题目内容
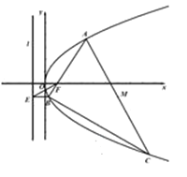
【题目】已知函数![]() .
.
(1)若函数![]() 有两个零点,证明:
有两个零点,证明:![]() ;
;
(2)设函数![]() 的两个零点为
的两个零点为![]() ,
,![]() .证明:
.证明:![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)参变分离可得![]() ,构造函数
,构造函数![]() ,判断
,判断![]() 的单调性及图象特征,使
的单调性及图象特征,使![]() 与直线
与直线![]() 有两个交点,即满足题意,从而可证明结论;
有两个交点,即满足题意,从而可证明结论;
(2)易知![]() ,
,![]() ,两式相减得
,两式相减得![]() ,要证
,要证![]() ,即证
,即证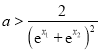 ,进而可将问题转化为证明
,进而可将问题转化为证明 ,令
,令![]() ,则
,则![]() ,即证
,即证![]() ,进而构造函数
,进而构造函数![]() ,只需证明
,只需证明![]() 即可.
即可.
(1)证明:由![]() ,可得
,可得![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
所以![]() .
.
又因为当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,且当
,且当![]() 时,
时,![]() ;
;
所以![]() 有两个零点时,
有两个零点时,![]() .
.
(2)由题意知,![]() ,
,![]() ,
,
两式相减得:![]() ,
,
则![]() .
.
要证![]() ,即证
,即证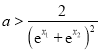 ,
,
只需证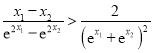 ,
,
即证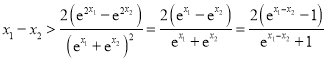 .
.
令![]() ,则
,则![]() ,即证
,即证![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
故![]() 成立.
成立.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: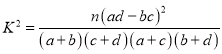 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,且保费与上一年度车辆发生道路交通事故的情况相联系.发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,且保费与上一年度车辆发生道路交通事故的情况相联系.发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元.且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆车,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
【题目】凤梨穗龙眼原产厦门,是厦门市的名果,栽培历史已有100多年.龙眼干的级别按直径![]() 的大小分为四个等级(如下表).
的大小分为四个等级(如下表).
|
|
|
|
|
级别 | 三级品 | 二级品 | 一级品 | 特级品 |
某商家为了解某农场一批龙眼干的质量情况,随机抽取了100个龙眼干作为样本(直径分布在区间![]() ),统计得到这些龙眼干的直径的频数分布表如下:
),统计得到这些龙眼干的直径的频数分布表如下:
|
|
|
|
|
|
频数 | 1 |
| 29 |
| 7 |
用分层抽样的方法从样本的一级品和特级品中抽取6个,其中一级品有2个.
(1)求![]() 、
、![]() 的值,并估计这批龙眼干中特级品的比例;
的值,并估计这批龙眼干中特级品的比例;
(2)已知样本中的100个龙眼干约500克,该农场有500千克龙眼干待出售,商家提出两种收购方案:
方案![]() :以60元/千克收购;
:以60元/千克收购;
方案![]() :以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
:以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
用样本的频率分布估计总体分布,哪个方案农场的收益更高?并说明理由.