题目内容
某林场去年底森林木材存量为a,从今年起以每年25%的增长率增长,同时每年冬天要砍伐木材量为x,为了实现经过20年达到木材存量至少翻两番(是最初的4倍)的目标,求x的最大值.(取lg2=0.3)
解:如不计砍掉部分,那么20年后,木材存量为a(1+25%)20,第1年砍掉部分如不被砍掉,则应增长为
x(1+25%)19,依次第2年,第3年,…,第19年为x(1+25%)18,x(1+25%)17,…,x(1+25%).
根据题意有
a(1+25%)20-x(1+25%)19-x(1+25%)18-…-2x(1+25%)-x≥
即a·(![]() )20-
)20-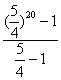 ·x≥
·x≥
而lg(![]() )20=20(lg5-lg4)=20(1-3lg2)=20(1-3×0.3)=2,
)20=20(lg5-lg4)=20(1-3lg2)=20(1-3×0.3)=2,
∴(![]() )20=102=100.
)20=102=100.
∴
解得x≤![]() a.
a.
∴x的最大值为![]() a.
a.

练习册系列答案
相关题目