题目内容
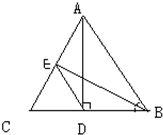 在△ABC中,AD是BC边上的高,垂足为D点.BE是∠ABC的角平分线,并交AC于E点.若BC=6,CA=7,AB=8.
在△ABC中,AD是BC边上的高,垂足为D点.BE是∠ABC的角平分线,并交AC于E点.若BC=6,CA=7,AB=8.(1)求DE的长;
(2)求△ABC的面积.
分析:(1)根据BE为角平分线,利用角平分线定理列出比例式,根据CA长求出CE与EA长,设CD为x,在直角三角形ACD与直角三角形ABD中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,过E作EF垂直于CD,求出CF与FD的长,进而求出EF的长,即可求出ED的长;
(2)利用余弦定理表示出cos∠ABC,将三角形三边长代入求出cos∠ABC的值,由∠ABC为三角形的内角,利用同角三角函数间的基本关系求出sin∠ABC的值,利用三角形的面积公式即可求出三角形ABC的面积.
(2)利用余弦定理表示出cos∠ABC,将三角形三边长代入求出cos∠ABC的值,由∠ABC为三角形的内角,利用同角三角函数间的基本关系求出sin∠ABC的值,利用三角形的面积公式即可求出三角形ABC的面积.
解答: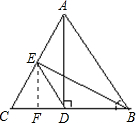 解:(1)∵BE为∠ABC的角平分线,
解:(1)∵BE为∠ABC的角平分线,
∴CE:EA=BC:BA=6:8,
∵CA=CE+EA=7,
∴CE=3,EA=4,
设CD=x,根据勾股定理得到CA2-x2=AD2=AB2-BD2,即49-x2=64-(6-x)2,
解得:x=
,
过E作EF⊥CD,可得CF:FD=CE:EA=3:4,CF+FD=CD=
,
∴CF=
,FD=1,
在Rt△CEF中,根据勾股定理得:EF=
=
=
,
在Rt△EFD中,根据勾股定理得:ED=
=
;
(2)∵BC=6,CA=7,AB=8,
∴cos∠ABC=
=
,
∵∠ABC为三角形的内角,
∴sin∠ABC=
=
=
,
则S△ABC=
BC•AB•sin∠ABC=
.
 解:(1)∵BE为∠ABC的角平分线,
解:(1)∵BE为∠ABC的角平分线,∴CE:EA=BC:BA=6:8,
∵CA=CE+EA=7,
∴CE=3,EA=4,
设CD=x,根据勾股定理得到CA2-x2=AD2=AB2-BD2,即49-x2=64-(6-x)2,
解得:x=
| 7 |
| 4 |
过E作EF⊥CD,可得CF:FD=CE:EA=3:4,CF+FD=CD=
| 7 |
| 4 |
∴CF=
| 3 |
| 4 |
在Rt△CEF中,根据勾股定理得:EF=
| CE2-CF2 |
9-
|
| ||
| 4 |
在Rt△EFD中,根据勾股定理得:ED=
| EF2+FD2 |
| ||
| 4 |
(2)∵BC=6,CA=7,AB=8,
∴cos∠ABC=
| 64+36-49 |
| 2×6×8 |
| 51 |
| 96 |
∵∠ABC为三角形的内角,
∴sin∠ABC=
1-(
|
| ||
| 96 |
3
| ||
| 96 |
则S△ABC=
| 1 |
| 2 |
3
| ||
| 4 |
点评:此题属于解三角形题型,涉及的知识有:勾股定理,角平分线定理,同角三角函数间的基本关系,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)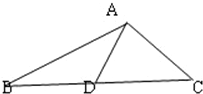 如图,在△ABC中,AD是BC边上的中线,AB=5,AC=3,AD=2,求:BC的长及面积S△ABC.
如图,在△ABC中,AD是BC边上的中线,AB=5,AC=3,AD=2,求:BC的长及面积S△ABC.