题目内容
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且 .
.
(1)求证:EF∥平面BDC1;
(2)求证: 平面
平面 .
.
证明见解析.
解析试题分析:(1)要证线面平行,就是要在平面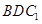 内找一条直线与直线
内找一条直线与直线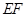 平行,本题中容易看出就是要证明
平行,本题中容易看出就是要证明  ,而这个在四边形
,而这个在四边形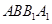 中只要取
中只要取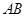 中点
中点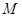 ,可证明
,可证明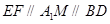 即得;(2)要证
即得;(2)要证 平面
平面 ,根据线面垂直的判定定理,就是要证
,根据线面垂直的判定定理,就是要证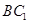 与平面
与平面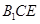 内的两条相交直线垂直,观察已知条件,正三棱柱的侧面是正方形,因此有
内的两条相交直线垂直,观察已知条件,正三棱柱的侧面是正方形,因此有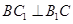 ,下面还要找一条垂线,最好在
,下面还要找一条垂线,最好在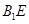 ,
, 中找一条,
中找一条,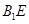 在平面
在平面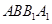 中,由平面几何知识易得
中,由平面几何知识易得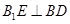 ,又由正三棱柱的性质可得
,又由正三棱柱的性质可得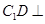 平面
平面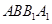 ,从而
,从而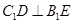 ,因此有
,因此有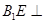 平面
平面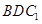 ,即有
,即有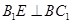 ,于是结论得证.
,于是结论得证.
(1)证明:取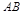 的中点M,因为
的中点M,因为 ,所以
,所以 为
为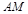 的中点,
的中点,
又因为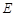 为
为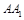 的中点,所以
的中点,所以 , 2分
, 2分
在正三棱柱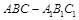 中,
中,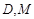 分别为
分别为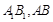 的中点,
的中点,
所以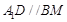 ,且
,且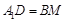 ,则四边形A1DBM为平行四边形,
,则四边形A1DBM为平行四边形,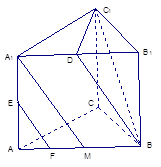
所以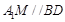 ,所以
,所以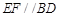 , 5分
, 5分
又因为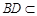 平面
平面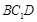 ,
,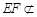 平面
平面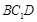 ,所以,
,所以,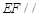 平面
平面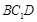 7分
7分
(2)连接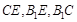 ,因为在正三角
,因为在正三角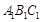 中,
中,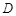 为
为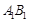 的中点,
的中点,
所以,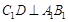 ,所以,在正三棱柱ABC-A1B1C1中,
,所以,在正三棱柱ABC-A1B1C1中,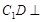 面
面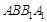 ,
,
所以, ,因为
,因为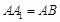 ,所以,四边形
,所以,四边形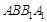 为正方形,由
为正方形,由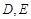 分别为
分别为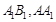 的中点,所以,可证得
的中点,所以,可证得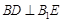 ,
,
所以,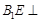 面
面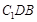 ,即
,即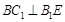 , 11分
, 11分
又因为在正方形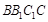 中,
中,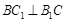 ,所以
,所以 面
面 , 14分
, 14分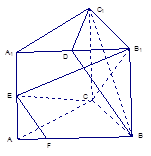
考点:线面平行与线面垂直.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 平面
平面 ,四边形
,四边形 为矩形,
为矩形, .
. 为
为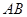 的中点,
的中点, .(1)求证:
.(1)求证: ;(2)若
;(2)若 与平面
与平面 所成的角为
所成的角为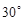 ,求二面角
,求二面角 的余弦值.
的余弦值.
 中,
中, ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,
, 分别为线段
分别为线段 的中点.
的中点.
 ;
;  ⊥平面
⊥平面 .
. 的大小为
的大小为 ,菱形
,菱形 在面
在面 内,
内,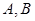 两点在棱
两点在棱 上,
上, ,
, 是
是 的中点,
的中点, 面
面 ,垂足为
,垂足为 .
. 平面
平面 ;
; 与
与 所成角的余弦值.
所成角的余弦值.
 是菱形,
是菱形, 是矩形,
是矩形, 面
面 .
.
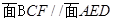 ;
; ,求四棱锥
,求四棱锥 的体积.
的体积. 中,
中, 为
为 上一点,面
上一点,面 面
面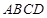 ,四边形
,四边形 为矩形
为矩形 ,
, ,
, .
. ,且
,且 ∥面
∥面 ,求
,求 的值;
的值; 面
面 ,并求点
,并求点 到面
到面 的距离.
的距离.
 中,底面
中,底面 是边长为
是边长为 的正方形,侧面
的正方形,侧面

 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
 平面
平面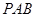
 ;
;  上是否存在点
上是否存在点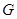 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?说明理由.
?说明理由. ,
, 为直角,
为直角, ,
, ,现以其中一直角边
,现以其中一直角边 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转 后,将
后,将 点所在的位置记为
点所在的位置记为 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转 后,
后, .
. ,取
,取 ,求证:面
,求证:面 面
面 ;
; 与平面
与平面
