题目内容
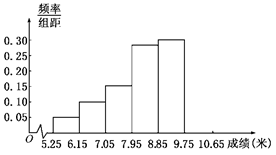
某高校组织的自主招生考试,共有1000名同学参加笔试,成绩均介于60分到100分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分为4组:第1组[60,70),第2组[70,80),第3组[80,90),第4组[90,100].如图是按上述分组方法得到的频率分布直方图,且笔试成绩在85分(含85分)以上的同学有面试资格.
(Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;
(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为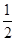 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
(Ⅰ)估计所有参加笔试的1000名同学中,有面试资格的人数;
(Ⅱ)已知某中学有甲、乙两位同学取得面试资格,且甲的笔试比乙的高;面试时,要求每人回答两个问题,假设甲、乙两人对每一个问题答对的概率均为
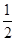 ;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.
;若甲答对题的个数不少于乙,则甲比乙优先获得高考加分资格.求甲比乙优先获得高考加分资格的概率.(Ⅰ)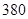 人;(Ⅱ)
人;(Ⅱ) .
.
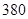 人;(Ⅱ)
人;(Ⅱ) .
.试题分析:(Ⅰ)先计算出
 内的频率,再计算出满足条件的频率乘以相应的总人数即可;(Ⅱ)应用列举法写出满足条件的所有情况,再找出甲答对题的个数不少于乙的情况数,利用古典概型求解.
内的频率,再计算出满足条件的频率乘以相应的总人数即可;(Ⅱ)应用列举法写出满足条件的所有情况,再找出甲答对题的个数不少于乙的情况数,利用古典概型求解.试题解析:(Ⅰ)设第
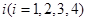 组的频率为
组的频率为 ,则由频率分布直方图知
,则由频率分布直方图知 (2分)
(2分)所以成绩在85分以上的同学的概率
P≈
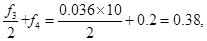 (5分)
(5分)故这1000名同学中,取得面试资格的约有
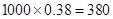 人. (6分)
人. (6分)(Ⅱ)设答对记为1,打错记为0,则所有可能的情况有:
甲00乙00,甲00乙10,甲00乙01,甲00乙11,甲10乙00,甲10乙10,甲10乙01,
甲10乙11,甲01乙00,甲01乙10,甲01乙01,甲01乙11,甲11乙00,甲11乙10,
甲11乙01,甲11乙11,共16个 (9分)
甲答对题的个数不少于乙的情况有:
甲00乙00,甲10乙00,甲10乙10,甲10乙01,甲01乙00,甲01乙10,甲01乙01,
甲11乙00,甲11乙01,甲11乙10,甲11乙11,共11个 (11分)
故甲比乙优先获得高考加分资格的概率为
 . (12分)
. (12分)
练习册系列答案
相关题目
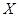 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求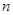 个学生体重的频率分布直方图,已知图中从左到右的前
个学生体重的频率分布直方图,已知图中从左到右的前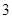 个小组的频率之比为
个小组的频率之比为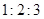 ,第
,第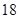 ,则的值
,则的值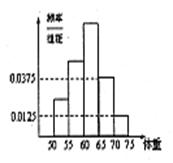


 的值是( )
的值是( )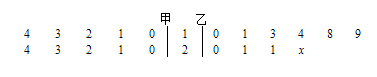

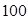 的样本的频率分布直方图见右图,则在区间
的样本的频率分布直方图见右图,则在区间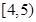 上的数据的频数为 .
上的数据的频数为 .
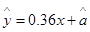 ,则根据此线性回归方程估计数学得90分的同学的物理成绩为 .(四舍五入到整数)
,则根据此线性回归方程估计数学得90分的同学的物理成绩为 .(四舍五入到整数)