题目内容
已知直线x+3y-7=0和kx-y-2=0与x轴、y轴所围成的四边形有外接圆，则实数k的值是 ．
【答案】分析：由直线x+3y-7=0和kx-y-2=0与x轴、y轴所围成的四边形有外接圆，得到对角之和为180°，又角AOB为90°，得到两直线的夹角为90°，即两直线垂直，根据两直线垂直时斜率的乘积为-1，分别表示出两直线的斜率相乘等于-1列出关于k的方程，求出的解即可得到实数k的值．
解答：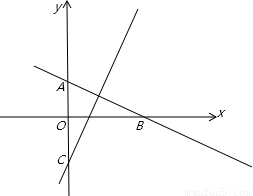
解：由图形可知：∠AOB=90°，
∴直线x+3y-7=0和kx-y-2=0的夹角为90°即两直线垂直，
又直线x+3y-7=0的斜率为-
，直线kx-y-2=0的斜率为k，
则-
k=-1，解得k=3．
故答案为：3
点评：此题考查学生四边形有外接圆的条件，掌握两直线垂直时斜率满足的关系，是一道基础题．
解答：
解：由图形可知：∠AOB=90°，∴直线x+3y-7=0和kx-y-2=0的夹角为90°即两直线垂直，
又直线x+3y-7=0的斜率为-
，直线kx-y-2=0的斜率为k，则-
k=-1，解得k=3．故答案为：3
点评：此题考查学生四边形有外接圆的条件，掌握两直线垂直时斜率满足的关系，是一道基础题．
练习册系列答案
相关题目