题目内容
【题目】设函数F（x）= 
，其中f（x）=log2（x2+1），g（x）=log2（|x|+7）．
（1）在实数集R上用分段函数形式写出函数F（x）的解析式；
（2）求函数F（x）的最小值．
【答案】
（1）
解：F（x）=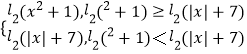 
，
令log2（x2+1）≥log2（|x|+7），得x2﹣|x|﹣6≥0，
解得：x≤﹣3或x≥3，（5分）∴F（x）=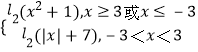 
（2）
解：当x≥3或x≤﹣3时，F（x）=log2（x2+1），设u=x2+1≥10，y=log2u在[10，+∞）上递增，所以F（x）min=log210；（说明：设元及单调性省略不扣分）
同理，当﹣3＜x＜3，F（x）min=log27；
又log27＜log210∴x∈R时，F（x）min=log27．
或解：因为F（x）是偶函数，所以只需要考虑x≥0的情形，
当0≤x＜3，F（x）=log2（x2+7），当x=0时，F（x）min=log27；
当x≥3时，F（x）=log2（x2+1），当x=3时，F（x）min=log210；
∴x∈R时，F（x）min=log27
【解析】（1）令log2（x2+1）≥log2（|x|+7），解得：x的取值范围，再结合F（x）的意义用分段函数形式写出函数F（x）的解析式即可；（2）先分情况讨论函数的单调性：当x≥3或x≤﹣3时；当﹣3＜x＜3，分别求出F（x）的最小值，最后综合得出x∈R时，F（x）min=log27．或利用F（x）的奇偶性，只需要考虑x≥0的情形，只须分两种情形讨论：当0≤x＜3，当x≥3时，分别求得F（x）的最小值即得．
【考点精析】关于本题考查的函数的值域，需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的才能得出正确答案．
