题目内容
2、函数y=f（x）在（0，2）上是增函数，函数y=f（x+2）是偶函数，则f（1），f（2.5），f（3.5）的大关系是（ ）
分析：根据函数y=f（x+2）是偶函数，知x=2是其对称轴，又函数y=f（x）在（0，2）上是增函数，可知其在（2，4）上为减函数，
而2.5，3.5∈（2，4），1∉（2，4），而f（1）=f（3），根据函数的单调性可得结果．
而2.5，3.5∈（2，4），1∉（2，4），而f（1）=f（3），根据函数的单调性可得结果．
解答：解：因为函数y=f（x）在（0，2）上是增函数，函数y=f（x+2）是偶函数，
所以x=2是对称轴，在（2，4）上为减函数，
f（2.5）＞f（1）=f（3）＞f（3.5）．
故选B．
所以x=2是对称轴，在（2，4）上为减函数，
f（2.5）＞f（1）=f（3）＞f（3.5）．
故选B．
点评：考查函数的奇偶性和单调性，并且根据函数的单调性比较函数值的大小，属基础题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
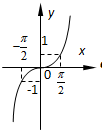已知函数y=f（x）的图象如图，则函数
