题目内容

已知数列{an}，an=2n2-10n+3，它的最小项是（　　）
分析：利用配方法，再根据数列中n的特点，即可确定数列的最大项．
解答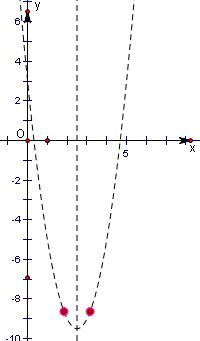：解：∵an=2n2-10n+3=2（n-
5
2
）2-
19
2
，
∵n∈N*，
∴n=2或3时，an为最小项，
即它的最小项是第二项或第三项．
故选D．
点评：本题考查数列的应用，考查配方法，属于基础题．
练习册系列答案
相关题目
已知数列{an}满足
a□1-1
2
+
a2-1
22
+…+
an-1
2n
=n2+n(n∈N*)．
（I）求数列{an}的通项公式；
（II）求数列{an}的前n项和Sn．
已知数列{an}满足a 1=
2
5
，且对任意n∈N*，都有
an
an+1
=
4an+2
an+1+2
．
（1）求证：数列{
1
an
}为等差数列，并求{an}的通项公式；
（2）令bn=an•an+1，Tn=b1+b2+b3+…+bn，求证：Tn＜
4
15
．
已知数列{an}满足a 1=
2
5
，且对任意n∈N+，都有
an
an+1
=
4an+2
an+1+2
．
（1）求{an}的通项公式；
（2）令bn=an•an+1，Tn=b1+b2+b3+…+bn，求证：Tn＜
4
15
．
已知数列{an}满足a n+an+1=
1
2
(n∈N+)，a 1=-
1
2
，Sn是数列{an}的前n项和，则S2013=
 
．
已知数列{an}:,,,…,,…,其中a是大于零的常数,记{an}的前n项和为Sn,计算S1,S2,S3的值,由此推出计算Sn的公式,并用数学归纳法加以证明.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网