题目内容
若三棱锥A-BCD侧面ABC内一动点P到BCD的距离与到棱AB的距离相等，则动点P的轨迹与△ABC组成的图形可能是（ ）
分析：设二面角A-BC-D的大小为θ，作PR⊥面BCD于R，PQ⊥BC于Q，PC⊥AB于T，则∠PQR=θ，由题设条件知
=sinθ为小于1的常数．
| PT |
| PQ |
解答：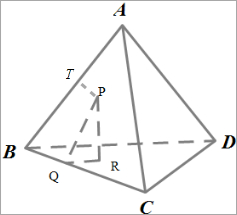
解：设二面角A-BC-D的大小为θ，如图．
作PR⊥面BCD于R，PQ⊥BC于Q，PC⊥AB于T，
则∠PQR=θ，
且由条件PT=PR=PQ•sinθ，
∴
=sinθ为小于1的常数，
即定点P的轨迹是直线，且直线与AB的夹角较小
分析四个答案中的图形，只有D满足要求
故选D．
解：设二面角A-BC-D的大小为θ，如图．作PR⊥面BCD于R，PQ⊥BC于Q，PC⊥AB于T，
则∠PQR=θ，
且由条件PT=PR=PQ•sinθ，
∴
| PT |
| PQ |
即定点P的轨迹是直线，且直线与AB的夹角较小
分析四个答案中的图形，只有D满足要求
故选D．
点评：本题考查轨迹方程问题，数形结合是最有效的解题方法．解答的关键是分析出动点P到直线AB与BC的距离之比为小于1的常数
练习册系列答案
相关题目
在三棱锥A-BCD中，已知侧面ABD⊥底面BCD，若∠ABC=60°，∠CBD=45°，则侧棱AB与底面BCD所成的角为（ ）| A、30° | B、45° | C、60° | D、75° |
如图空间四边形ABCD中，AC=4，BD=2，E，F分别是BC和AD的中点．
底面BCD，若
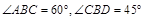，则侧棱AB与底面BCD所 成的角为
．