题目内容
(本小题满分12分)
如图:四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB= ,E、F分别为线段PD和BC的中点.
,E、F分别为线段PD和BC的中点.
(Ⅰ) 求证:CE∥平面PAF;
(Ⅱ) 在线段BC上是否存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°?若存在,试确定G的位置;若不存在,请说明理由.
(1)取PA中点为H,连结CE、HE、FH,证出HE∥AD,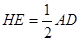 ,
,
由ABCD是平行四边形,且F为线段BC的中点 推出FC∥AD,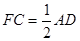 ,
,
从而进一步得出CE∥平面PAF;
(2)线段BC上存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°点G即为B点
解析试题分析:证明(1)取PA中点为H,连结CE、HE、FH,
因为H、E分别为PA、PD的中点,所以HE∥AD,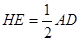 ,
,
因为ABCD是平行四边形,且F为线段BC的中点 所以FC∥AD,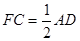
所以HE∥FC,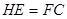 四边形FCEH是平行四边形 所以EC∥HF
四边形FCEH是平行四边形 所以EC∥HF
又因为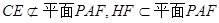
所以CE∥平面PAF ……………4分
(2)因为四边形ABCD为平行四边形且∠ACB=90°,
所以CA⊥AD 又由平面PAD⊥平面ABCD可得
CA⊥平面PAD 所以CA⊥PA
由PA=AD=1,PD= 可知,PA⊥AD…………5分
可知,PA⊥AD…………5分
所以可建立如图所示的平面直角坐标系A-xyz
因为PA=BC=1,AB= 所以AC=1 所以
所以AC=1 所以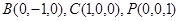
假设BC上存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°,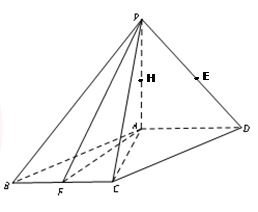 设点G的坐标为(1,a,0),
设点G的坐标为(1,a,0),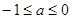 所以
所以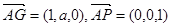
设平面PAG的法向量为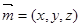
则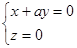 令
令 所以
所以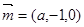
又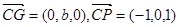
设平面PCG的法向量为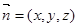
则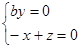 令
令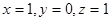 所以
所以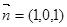 ……………9分
……………9分
因为平面PAG和平面PGC所成二面角的大小为60°,所以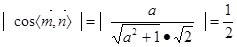
所以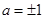 又
又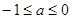 所以
所以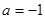 ……………11分
……………11分
所以线段BC上存在一点G,使得平面PAG和平面PGC所成二面角的大小为60°点G即为B点……12分
考点:本题主要考查立体几何中的平行关系、垂直关系,角的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。本题利用向量简化了证明过程。把证明问题转化成向量的坐标运算,这种方法带有方向性。

 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
, ,
, ,
,  是
是 的中点.
的中点.
 平面
平面 ;
; ;
; 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点,  ,且
,且 .将梯形
.将梯形 折成直二面角
折成直二面角 ,如图2所示.
,如图2所示.
 平面
平面 ;
; 关于点
关于点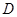 的对称点为
的对称点为 ,点
,点 在
在 所在平面内,且直线
所在平面内,且直线 与平面
与平面 所成的角为
所成的角为 ,试求出点
,试求出点 的最短距离.
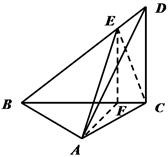
的最短距离.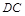 ⊥平面
⊥平面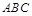 ,
,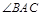 =90°,
=90°,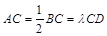 ,点
,点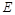 在
在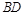 上,点E在BC上的射影为F,且
上,点E在BC上的射影为F,且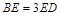 .
.
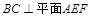 ;
;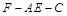 的大小为45°,求
的大小为45°,求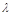 的值.
的值.
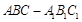 中,
中, ,
,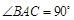 .
.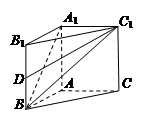
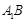 与
与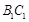 所成的角为
所成的角为 ,求棱柱的高;
,求棱柱的高;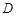 是
是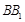 的中点,
的中点,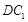 与平面
与平面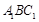 所成的角为
所成的角为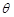 ,当棱柱的高变化时,求
,当棱柱的高变化时,求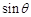 的最大值.
的最大值. 中,
中, 为
为 边上的高,
边上的高, ,
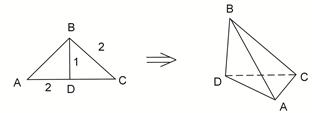
, ,沿
,沿 翻折,使得
翻折,使得 ,得到几何体
,得到几何体 。
。
 ;
; 与平面
与平面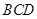 所成角的正切值。
所成角的正切值。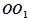 与三棱柱
与三棱柱 的组合体,其中,圆柱
的组合体,其中,圆柱 是边长为4的正方形,
是边长为4的正方形,
 为等腰直角三角形,
为等腰直角三角形, .
.
 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE =
,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE = ,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
 ,求
,求