题目内容
若直线4x-3y-2=0与圆x2+y2-2ax+4y+a2-12=0总有两个不同交点,则a的取值范围是
| A.-3<a<7 | B.-6<a<4 |
| C.-7<a<3 | D.-21<a<19 |
B
解析

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
点 在圆
在圆 内,则直线
内,则直线 和已知圆的公共点个数为
和已知圆的公共点个数为
| A.0 | B.1 | C.2 | D.不能确定 |
圆 与圆
与圆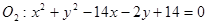 的位置关系是( )
的位置关系是( )
| A.相离 | B.内含 | C.外切 | D.内切 |
圆 的圆心坐标为( )
的圆心坐标为( )
A. | B. | C. | D. |
设直线 过点
过点 ,且与圆
,且与圆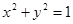 相切,则
相切,则 的斜率是( )
的斜率是( )
A. | B. | C. | D.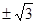 |
过点 作直线
作直线 与圆
与圆 相交于
相交于 两点,那么
两点,那么 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
直线 与圆
与圆 的位置关系为( )
的位置关系为( )
| A.相切 | B.相交但直线不过圆心 |
| C.直线过圆心 | D.相离 |
若函数 的图象在点
的图象在点 处的切线
处的切线 与圆
与圆 相交,则点
相交,则点 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.圆内 | B.圆内或圆外 | C.圆上 | D.圆外 |
点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是 ( )
| A.|a|<1 | B.a< | C.|a|< | D.|a|< |