题目内容
若x,y满足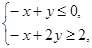 则
则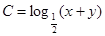 的最大值为 .
的最大值为 .
-2
解析试题分析:作出不等式所表示的平面区域: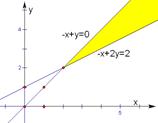 ,由此可知x+y在点P(2,2)处取得最小值为4,又因为函数
,由此可知x+y在点P(2,2)处取得最小值为4,又因为函数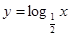 在(0,
在(0, )上是减函数,所以CMAX=
)上是减函数,所以CMAX=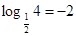 ,故应填入-2.
,故应填入-2.
考点:1.线性规划;2.对数函数的单调性.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
(2011德州模拟)某运输公司有12名驾驶员和19名工人,有8辆载重量为10
吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需运往 地至少72吨的货物,派用的
地至少72吨的货物,派用的
每辆车需满载且只运送一次.派用的每辆甲型卡车需配2名工人,运送一次可得利润450
元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元,该公司合理计划当天派
用两类卡车的车辆数,可得最大利润为( )
| A.4650元 | B.4700元 | C.4900元 | D.5000元 |
下列给出的四个点中,位于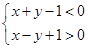 表示的平面区域内的点是 ( )
表示的平面区域内的点是 ( )
A.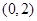 | B.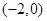 | C.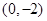 | D.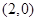 |
设 满足约束条件
满足约束条件 ,则
,则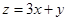 的最大值为 ( )
的最大值为 ( )
| A.5 | B.3 | C.7 | D.-8 |
设点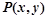 满足:
满足: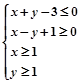 ,则
,则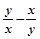 的取值范围是 ( )
的取值范围是 ( )
A.[ | B.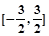 | C. | D.[-1,1] |
 ,则z=2x+y的最大值为 _________ .
,则z=2x+y的最大值为 _________ .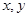 满足约束条件
满足约束条件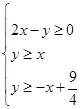 ,则
,则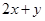 的最小值为 .
的最小值为 .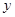 满足和
满足和 ,则
,则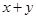 的取值范围是________.
的取值范围是________. 若z=x2+y2,则z的最大值为________.
若z=x2+y2,则z的最大值为________.