题目内容
已知平面向量
=（
sinx，cosx），
=（cosx，cosx），x∈（0，π〕，若f（x）=•
（1）求f（
）的值；
（2）求f（x）的最大值及相应的x的值．
解：（1）∵f（x）=•
=sinxcosx+cos2x
=
sin2x+
=sin（2x+
）+
，
∴f（）=sin（2×+）+
=-sin+
=-+．
（2）∵f（x）=sin（2x+）+
∴当2x+=+2kπ（k∈Z）
即x=
+kπ（k∈Z）时
有f（x）max=1+=
．
分析：（1）由题意可求得f（x）=•=sin（2x+）+，从而可求得求f（）的值；
（2）由f（x）=sin（2x+）+，可求得f（x）的最大值及相应的x的值．
点评：本题考查三角函数的化简求值，着重考查平面向量数量积的运算及正弦函数的性质，属于中档题．
•=
sinxcosx+cos2x=
sin2x+=sin（2x+
）+，∴f（
）=sin（2×+）+=-sin
+=-
+．（2）∵f（x）=sin（2x+
）+∴当2x+
=+2kπ（k∈Z）即x=
+kπ（k∈Z）时有f（x）max=1+
=．分析：（1）由题意可求得f（x）=
•=sin（2x+）+，从而可求得求f（）的值；（2）由f（x）=sin（2x+
）+，可求得f（x）的最大值及相应的x的值．点评：本题考查三角函数的化简求值，着重考查平面向量数量积的运算及正弦函数的性质，属于中档题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
=（
，-1），
=（sinx，cosx）
⊥
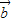，求tanx的值
•
，求f（x）的最大值及取得最大值的x的取值集合．