Question

河上有抛物线型拱桥，当水面距拱顶5米时，水面宽度为8米，一小船宽4米，高2米，载货后船露出水面的部分高0.75米，问水面上涨到与抛物线拱顶距多少时，小船开始不能通行？

Answer 1

分析：建立平面直角坐标系，设拱桥型抛物线方程为x²=-2py（p＞0）．将B（4，-5）代入得p=1.6，所以x²=-3.2y，当船两侧与抛物线接触时不能通过，由此能求出结果．

解答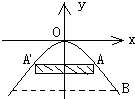：解：建立平面直角坐标系，
设拱桥型抛物线方程为x²=-2py（p＞0）．…（2分）
将B（4，-5）代入得p=1.6，
∴x²=-3.2y，…（6分）
当船两侧与抛物线接触时不能通过，
设点A（2，y_A），
由2²=-3.2 y_A，
得y_A=-1.25，…（10分）
因为船露出水面的部分高0.75米，…（12分）
所以h=|y_A|+0.75=2米．…（14分）
答：水面上涨到与抛物线拱顶距2米时，小船开始不能通行．…（16分）

点评：本题考查抛物线的应用，是中档题．解题时要认真审题，恰当地建立坐标系，合理地进行等价转化．