题目内容
某河上有抛物线型拱桥,当水面距拱顶5 m时,水面宽8 m,一木船宽4 m,高2 m,载货后木船露在水面上的部分高为
解析:求抛物线方程时,若由已知条件可知曲线是抛物线,一般用待定系数法.?
本题中影响通航的因素是高度和宽度,而宽度是首要的,据对称性,可取拱顶为坐标原点,拱桥的对称轴为y轴建立直角坐标系xOy,设抛物线方程为x2=-2py(p>0),运用待定系数法确定参数p,问题即可获解.
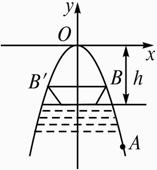
解:根据题意,建立图所示的直角坐标系,设抛物线方程为x2=-2py(p>0),
∵A(4,-5)在抛物线上,?
∴42=-2p(-5),p=1.6.?
∴x2=-3.2y(-4≤x≤4).?
设当水面BB′上涨到与抛物线拱顶相距h米时船开始不能通航,这时木船两侧与抛物线接触,于是可设木船宽BB′的端点B的坐标为(2,y1),由22=-3.2y1,得y1=-![]() ,h=|y1|+
,h=|y1|+![]() =|-
=|-![]() |+
|+![]() =2(m),所以当水面上涨到与抛物线拱顶相距2 m时,船开始不能通航.
=2(m),所以当水面上涨到与抛物线拱顶相距2 m时,船开始不能通航.

练习册系列答案
相关题目
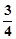 m,则水面上涨到与抛物线拱顶相距
m,则水面上涨到与抛物线拱顶相距