题目内容
设M为平面内一些向量组成的集合,若对任意正实数t和向量a∈M,都有ta∈M,则称M为“点射域”.现有下列平面向量的集合:
①{(x,y)|x2≥y};
②{(x,y)|
};
③{(x,y)|x2+y2-2x≥0};
④{(x,y)|3x2+2y2-6<0}.
上述为“点射域”的集合有
①{(x,y)|x2≥y};
②{(x,y)|
|
③{(x,y)|x2+y2-2x≥0};
④{(x,y)|3x2+2y2-6<0}.
上述为“点射域”的集合有
②
②
(写出所有正确命题的序号).分析:根据“点射域”的定义,分别推导t
∈M是否成立.
| a |
解答:解:设
=(x,y),则t
=(tx.ty).
①若
∈{(x,y)|x2≥y};若t
∈{(x,y)|x2≥y},即(tx)2≥ty,
因为t>0,整理得tx2≥y.显然当t≠1时,tx2≥y与x2≥y不是同解不等式,所以①不是“点射域”.
②若
∈{(x,y)|
},则有
,若t
∈{(x,y)|
},则有
,
因为t>0,所以不等式等价为
,由题意可知②是“点射域”.
③若
∈{(x,y)|x2+y2-2x≥0},则x2+y2-2x≥0,若t
∈{(x,y)|x2+y2-2x≥0},则有(tx)2+(ty)2-2tx≥0,
因为t>0,所以不等式等价tx2+ty2-2x≥0,显然当t≠1时,两不等式不是同解不等式,所以③不是“点射域”.
④若
∈{(x,y)|3x2+2y2-6<0},则有3x2+2y2-6<0.若t
∈{(x,y)|3x2+2y2-6<0},
则3(tx)2+2(ty)2-6<0,显然当t≠1时,两不等式不是同解不等式,所以④不是“点射域”.
故答案为:②.
| a |
| a |
①若
| a |
| a |
因为t>0,整理得tx2≥y.显然当t≠1时,tx2≥y与x2≥y不是同解不等式,所以①不是“点射域”.
②若
| a |
|
|
| a |
|
|
因为t>0,所以不等式等价为
|
③若
| a |
| a |
因为t>0,所以不等式等价tx2+ty2-2x≥0,显然当t≠1时,两不等式不是同解不等式,所以③不是“点射域”.
④若
| a |
| a |
则3(tx)2+2(ty)2-6<0,显然当t≠1时,两不等式不是同解不等式,所以④不是“点射域”.
故答案为:②.
点评:本题主要考查了新定义的应用,正确理解新定义的信息,并按照定义进行推导是解决这类问题的关键,综合性较强,难度较大.

练习册系列答案
相关题目
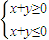 };
};