题目内容
设M为平面内一些向量组成的集合,若对任意正实数λ和向量
∈M,都有λ
∈M,则称M为“点射域”,则下列平面向量的集合为“点射域”的是( )
| a |
| a |
分析:根据题中“点射域”的定义对各个选项依次加以判别.
解答:解:根据“点射域”的定义,可得向量
∈M 时,与它共线的向量λ
∈M也成立,
A:{(x,y)|y≥x2}表示终点在抛物线y≥x2上及其张口以内的向量构成的区域,向量
=(1,1)∈M,但3
=(3,3)∉M,故它不是“点射域”;
B.表示终点在圆x2+(y-1)2=1上及其外部的向量构成的区域,向量
=(0,2)∈M,但
=(0,1)∉M,故它不是“点射域”;
C.可得任意正实数λ和向量
∈M,都有λ
∈M,故它是“点射域”;
D.表示终点在椭圆 3x2+2y2=12的向量构成的区域,向量
=(1,1)∈M,但3
=(3,3)∉M,故它不是“点射域”.
故选C.
| a |
| a |
A:{(x,y)|y≥x2}表示终点在抛物线y≥x2上及其张口以内的向量构成的区域,向量
| a |
| a |
B.表示终点在圆x2+(y-1)2=1上及其外部的向量构成的区域,向量
| a |
| 1 |
| 2 |
| a |
C.可得任意正实数λ和向量
| a |
| a |
D.表示终点在椭圆 3x2+2y2=12的向量构成的区域,向量
| a |
| a |
故选C.
点评:本题考查新定义的理解和应用,着重考查集合与元素的关系和向量的性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
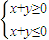 };
};