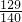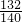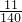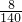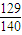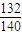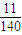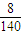题目内容
在坐标平面上,从满足1≤x≤3,1≤y≤3,且x,y是整数的点(x,y)中任意取出三个不同的点,则此三点构成三角形的概率是
- A.

- B.
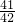
- C.
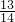
- D.
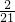
A
分析:由题意可得整点(x,y)共有9个,从9个点中任意取出三个不同的点共有C93=84个取法,若三点构成三角形,即三点不共线,三点共线的有8种取法,则不共线有C39-8=76中取法,再根据有关的公式可得答案.
解答:由题意可得:(x,y)为x,y是整数的点,1≤x≤3,1≤y≤3,
所以可以用网格表示,如图所示:
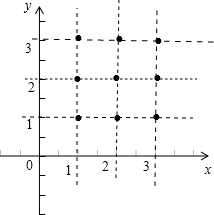
所以由图象可得整点(x,y)共有9个,
所以从9个点中任意取出三个不同的点共有C93=84个取法,
若此三点构成三角形,即三点不共线,
因为三点共线的有8种取法,
所以此时共有C39-8=76中取法,
所以此三点构成三角形的概率是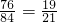 .
.
故选A.
点评:本题主要是考查古典概型,解决此类问题的关键是根据排列与组合正确的计算出基本事件总,再计算出符合条件的基本事件数,在计算时要做到不重不漏,进而根据古典概率模型的公式可得答案.
分析:由题意可得整点(x,y)共有9个,从9个点中任意取出三个不同的点共有C93=84个取法,若三点构成三角形,即三点不共线,三点共线的有8种取法,则不共线有C39-8=76中取法,再根据有关的公式可得答案.
解答:由题意可得:(x,y)为x,y是整数的点,1≤x≤3,1≤y≤3,
所以可以用网格表示,如图所示:

所以由图象可得整点(x,y)共有9个,
所以从9个点中任意取出三个不同的点共有C93=84个取法,
若此三点构成三角形,即三点不共线,
因为三点共线的有8种取法,
所以此时共有C39-8=76中取法,
所以此三点构成三角形的概率是
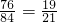 .
.故选A.
点评:本题主要是考查古典概型,解决此类问题的关键是根据排列与组合正确的计算出基本事件总,再计算出符合条件的基本事件数,在计算时要做到不重不漏,进而根据古典概率模型的公式可得答案.

练习册系列答案
相关题目