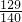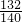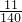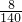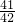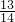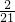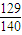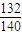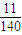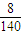题目内容
在坐标平面上,从满足1≤x≤4,1≤y≤4,且x,y是整数的点(x,y)中任意取出三个不同的点,则此三点构成三角形的概率是( )
分析:由题意可得:在1≤x≤4,1≤y≤4中存在的整数点(x,y)共有16个,可得从这些整数点中任意取出三个不同的点的取法有C163=560种.由题意可得:从中任意取出三个不同的点则此三点共线的取法有:44种,此三点不共线的取法有:560-44=516种,进而计算出此三点构成三角形的概率.
解答:解:由题意可得:在1≤x≤4,1≤y≤4中存在的整数点(x,y)共有16个,
所以从这些整数点中任意取出三个不同的点的取法有C163=560种.
若从中任意取出三个不同的点能够构成三角形,则此三点不共线,
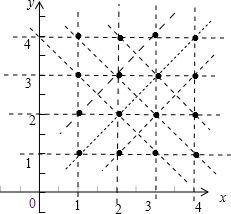
所以由图所示:从中任意取出三个不同的点则此三点共线的取法有:44种,
所以此三点不共线的取法有:560-44=516种,
所以此三点构成三角形的概率是:
=
.
故选A.
所以从这些整数点中任意取出三个不同的点的取法有C163=560种.
若从中任意取出三个不同的点能够构成三角形,则此三点不共线,

所以由图所示:从中任意取出三个不同的点则此三点共线的取法有:44种,
所以此三点不共线的取法有:560-44=516种,
所以此三点构成三角形的概率是:
| 516 |
| 560 |
| 129 |
| 140 |
故选A.
点评:本题主要是借助于三角形成立的条件考查古典概型,解决此类问题的关键是根据排列与组合正确的计算出基本事件总,再计算出符合条件的基本事件数,在计算时要做到不重不漏,进而根据古典概率模型的公式可得答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目