题目内容
4.试判断下列函数的奇偶性.(1)f(x)=1-2cosx+|tanx|:
(2)f(x)=x2tanx-sin2x.
分析 确定函数的定义域,利用函数的奇偶性的定义,即可得出结论.
解答 解:(1)函数的定义域为{x|x≠$\frac{π}{2}$+kπ,k∈Z},
f(-x)=1-2cos(-x)+|tan(-x)|=1-2cosx+|tanx|=f(x),
∴函数是偶函数;
(2)函数的定义域为{x|x≠$\frac{π}{2}$+kπ,k∈Z},
f(-x)=(-x)2tan(-x)-sin2(-x)=-(x2tanx-sin2x)=-f(x),
∴函数是奇函数.
点评 本题考查函数的奇偶性,正确运用函数的奇偶性的定义是关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
12. 如图,三棱台ABC-A1B1C1中,A1B1:AB=1:2,则三棱锥B-A1B1C1与三棱锥A1-ABC的体积之比为( )
如图,三棱台ABC-A1B1C1中,A1B1:AB=1:2,则三棱锥B-A1B1C1与三棱锥A1-ABC的体积之比为( )
 如图,三棱台ABC-A1B1C1中,A1B1:AB=1:2,则三棱锥B-A1B1C1与三棱锥A1-ABC的体积之比为( )
如图,三棱台ABC-A1B1C1中,A1B1:AB=1:2,则三棱锥B-A1B1C1与三棱锥A1-ABC的体积之比为( )| A. | 1:2 | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:4 |
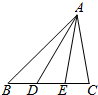 如图,D、E分别是△ABC的边BC的三等分点,设$\overrightarrow{AB}$=m,$\overrightarrow{AC}$=n,∠BAC=$\frac{π}{3}$.
如图,D、E分别是△ABC的边BC的三等分点,设$\overrightarrow{AB}$=m,$\overrightarrow{AC}$=n,∠BAC=$\frac{π}{3}$.