题目内容
19.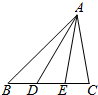 如图,D、E分别是△ABC的边BC的三等分点,设$\overrightarrow{AB}$=m,$\overrightarrow{AC}$=n,∠BAC=$\frac{π}{3}$.
如图,D、E分别是△ABC的边BC的三等分点,设$\overrightarrow{AB}$=m,$\overrightarrow{AC}$=n,∠BAC=$\frac{π}{3}$.(1)用$\overrightarrow{m}$、$\overrightarrow{n}$分别表示$\overrightarrow{AD}$,$\overrightarrow{AE}$;
(2)若$\overrightarrow{AD}$•$\overrightarrow{AE}$=15,|$\overrightarrow{BC}$|=3$\sqrt{3}$,求△ABC的面积.
分析 (1)$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}$,$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$,代入可得$\overrightarrow{AD}$;同理可得:$\overrightarrow{AE}$.
(2)$|\overrightarrow{m}|$=c,$|\overrightarrow{n}|$=b.由$\overrightarrow{AD}$•$\overrightarrow{AE}$=15,|$\overrightarrow{BC}$|=3$\sqrt{3}$,∠BAC=$\frac{π}{3}$.分别利用数量积运算性质、余弦定理可得bc,再利用三角形面积计算公式即可得出.
解答 解:(1)$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}$,$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC}$,$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$,∴$\overrightarrow{AD}$=$\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$=$\frac{2}{3}\overrightarrow{m}+\frac{1}{3}\overrightarrow{n}$;
同理可得:$\overrightarrow{AE}$=$\frac{1}{3}$$\overrightarrow{m}+\frac{2}{3}\overrightarrow{n}$.
(2)$|\overrightarrow{m}|$=c,$|\overrightarrow{n}|$=b.
∵$\overrightarrow{AD}$•$\overrightarrow{AE}$=15,|$\overrightarrow{BC}$|=3$\sqrt{3}$,
∴$(\frac{2}{3}\overrightarrow{m}+\frac{1}{3}\overrightarrow{n})$•$(\frac{1}{3}\overrightarrow{m}+\frac{2}{3}\overrightarrow{n})$=$\frac{2}{9}{\overrightarrow{m}}^{2}$+$\frac{2}{9}{\overrightarrow{n}}^{2}$+$\frac{5}{9}\overrightarrow{m}•\overrightarrow{n}$=$\frac{2}{9}{c}^{2}$+$\frac{2}{9}$b2+$\frac{5}{9}$bccos$\frac{π}{3}$=$\frac{2}{9}{c}^{2}$+$\frac{2}{9}$b2+$\frac{5}{18}$bc=15,
$(3\sqrt{3})^{2}$=${b}^{2}+{c}^{2}-2bccos\frac{π}{3}$,化为b2+c2-bc=27.
∴bc=18.
∴S△ABC=$\frac{1}{2}bcsinA$=$\frac{1}{2}×18×\frac{\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{2}$.
点评 本题考查了数量积运算性质、余弦定理、三角形面积计算公式、向量三角形法则,考查了推理能力与计算能力,属于中档题.

| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | c<a<b |
| A. | (2,0)或(4,6) | B. | (2,0)或(6,4) | C. | (4,6) | D. | (0,2) |
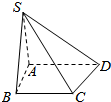 如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,CD=$\sqrt{5}$.
如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,CD=$\sqrt{5}$.