题目内容
f(x)=|2x-1|,f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn-1(x)),则函数y=f4(x)的零点个数为________.
8
分析:由递推的函数式,逐层求解,获得方程的根,即为函数的零点,可得个数.
解答:由题意可得y=f4(x)=f(f3(x))=|2f3(x)-1|,
令其为0可得f3(x)= ,即f(f2(x))=|2f2(x)-1|=
,即f(f2(x))=|2f2(x)-1|= ,
,
解得f2(x)= 或f2(x)=
或f2(x)= ,即f(f1(x))=
,即f(f1(x))= 或
或 ,
,
而f(f1(x))=|2f1(x)-1|,令其等于 或
或 ,
,
可得f1(x)= ,或
,或 ;或
;或 ,或
,或 ,
,
由f1(x)=f(x)=|2x-1|= ,或
,或 ;或
;或 ,或
,或 ,
,
可解得x= 或
或 ;
; 或
或 ;
; 或
或 ;
;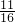 或
或 .
.
故可得函数y=f4(x)的零点个数为:8
故答案为8
点评:本题考查根的存在性及个数的判断,逐层突破是解决问题的关键,属中档题.
分析:由递推的函数式,逐层求解,获得方程的根,即为函数的零点,可得个数.
解答:由题意可得y=f4(x)=f(f3(x))=|2f3(x)-1|,
令其为0可得f3(x)=
 ,即f(f2(x))=|2f2(x)-1|=
,即f(f2(x))=|2f2(x)-1|= ,
,解得f2(x)=
 或f2(x)=
或f2(x)= ,即f(f1(x))=
,即f(f1(x))= 或
或 ,
,而f(f1(x))=|2f1(x)-1|,令其等于
 或
或 ,
,可得f1(x)=
 ,或
,或 ;或
;或 ,或
,或 ,
,由f1(x)=f(x)=|2x-1|=
 ,或
,或 ;或
;或 ,或
,或 ,
,可解得x=
 或
或 ;
; 或
或 ;
; 或
或 ;
;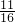 或
或 .
.故可得函数y=f4(x)的零点个数为:8
故答案为8
点评:本题考查根的存在性及个数的判断,逐层突破是解决问题的关键,属中档题.

练习册系列答案
相关题目