Question

设函数f（x）=|2x+1|-|x-4|．
（ I）画出函数y=f（x）的图象．
（ II）求函数y=f（x）的最小值．

Answer 1

分析：（I）利用零点分段法，化简函数，可得分段函数，从而可作出函数的图象；
（II）根据图象可求函数y=f（x）的最小值．

解答：解：（I）利用零点分段法，化简函数f（x）=|2x+1|-|x-4|=

-x-5，x＜- 1 2 3x-3，- 1 2 ≤x≤4 x+5，x＞4

，函数的图象如图所示

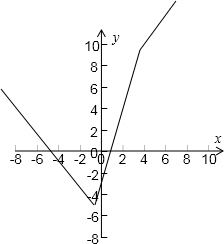
（II）根据图象可知，x=-

1

2

时，函数y=f（x）取得最小值-4

1

2

．

点评：本题考查函数图象的作法，考查分段函数，考查利用函数图象求函数的最值，正确作出函数的图象是关键．