题目内容
已知-1<a<0,则三个数 由小到大的顺序是 .
由小到大的顺序是 .
【答案】分析:由指数函数y=3x图象和性质,且-1<a<0可得到 ,再由指数函数y=ax(0<a<1)在定义域上是单调递减函数
,再由指数函数y=ax(0<a<1)在定义域上是单调递减函数
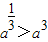 ,当-1<a<0时,则有
,当-1<a<0时,则有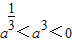 ,从而得到结论.
,从而得到结论.
解答:解:由指数函数y=3x图象和性质
-1<a<0
得: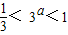
∵指数函数y=ax(0<a<1)在定义域上是单调递减函数
∴
-1<a<0时
∴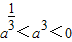
故有: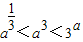
故答案为: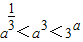
点评:本题主要考查指数函数的图象和性质,一般来讲,数的比较往往转化为函数的单调性或借助0.1等作为桥梁解决.
 ,再由指数函数y=ax(0<a<1)在定义域上是单调递减函数
,再由指数函数y=ax(0<a<1)在定义域上是单调递减函数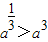 ,当-1<a<0时,则有
,当-1<a<0时,则有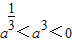 ,从而得到结论.
,从而得到结论.解答:解:由指数函数y=3x图象和性质
-1<a<0
得:
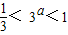
∵指数函数y=ax(0<a<1)在定义域上是单调递减函数
∴

-1<a<0时
∴
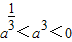
故有:
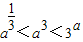
故答案为:
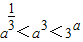
点评:本题主要考查指数函数的图象和性质,一般来讲,数的比较往往转化为函数的单调性或借助0.1等作为桥梁解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 由小到大的顺序是 .
由小到大的顺序是 . 由小到大的顺序是 .
由小到大的顺序是 . 由小到大的顺序是 .
由小到大的顺序是 .