题目内容
已知等差数列{an}中，Sn是它前n项和，设a6=2，S10=10．（1）求数列{an}的通项公式；
（2）若从数列{an}中依次取出第2项，第4项，第8项，…，第2n项，…，按取出的顺序组成一个新数列{bn}，试求数列{bn}的前n项和Tn．
【答案】分析：（1）设数列{an}首项，公差分别为a1，d．进而根据等差数列的通项公式和求和公式表示出a6和S10，联立方程求得a1和d，则数列的通项公式可得．
（2）依题意可知bn=a2n，进而根据（1）中数列的通项公式求得bn，进而利用等比数列的求和公式求得答案．
解答：解：（1）设数列{an}首项，公差分别为a1，d．
则由已知得a1+5d=2①
10a1+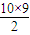
d=10②
联立①②解得a1=-8，d=2，
所以an=2n-10（n∈N*）．
（2）bn=a2n=2•2n-10=2n+1-10（n∈N*），
所以Tn=b1+b2+…+bn=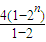
-10n=2n+2-10n-4．
点评：本题主要考查了等差数列的通项公式和等比数列的求和公式的应用．作为数列的基本知识，平时应注意多记忆．
（2）依题意可知bn=a2n，进而根据（1）中数列的通项公式求得bn，进而利用等比数列的求和公式求得答案．
解答：解：（1）设数列{an}首项，公差分别为a1，d．
则由已知得a1+5d=2①
10a1+
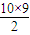d=10②联立①②解得a1=-8，d=2，
所以an=2n-10（n∈N*）．
（2）bn=a2n=2•2n-10=2n+1-10（n∈N*），
所以Tn=b1+b2+…+bn=
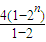-10n=2n+2-10n-4．点评：本题主要考查了等差数列的通项公式和等比数列的求和公式的应用．作为数列的基本知识，平时应注意多记忆．
练习册系列答案
相关题目
已知等差数列{an}中，a4a6=-4，a2+a8=0，n∈N*．