题目内容
设F1(-c,0)、F2(c,0)是椭圆 +
+ =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为( )
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为( )A.

B.

C.

D.

【答案】分析:根据题意可知∠F1PF2=90°,∠PF1F2=5∠PF2F1,进而求得∠PF1F2和∠PF2F1,在Rt△PF1F2分别表示出|PF1|和|PF2|,进而根据椭圆的定义表示出a,进而求得a和c的关系,即椭圆的离心率.
解答:解:∵P是以F1F2为直径的圆与椭圆的一个交点,
∴∠F1PF2=90°
∵∠PF1F2=5∠PF2F1,
∴∠PF1F2=15°,∠PF2F1=75°
∴|PF1|=|F1F2|sin∠PF2F1=2c•sin75°,∴|PF2|=|F1F2|sin∠PF1F2=2c•sin15°,
∴2a=|PF1|+|PF2|=2c•sin75°+2c•sin15°=4csin45°cos30°= c
c
∴a= c
c
∴e= =
=
故选B.
点评:本题主要考查了椭圆的简单性质.涉及了圆的性质,解三角形问题等.考查了学生综合分析问题的能力.
解答:解:∵P是以F1F2为直径的圆与椭圆的一个交点,
∴∠F1PF2=90°
∵∠PF1F2=5∠PF2F1,
∴∠PF1F2=15°,∠PF2F1=75°
∴|PF1|=|F1F2|sin∠PF2F1=2c•sin75°,∴|PF2|=|F1F2|sin∠PF1F2=2c•sin15°,
∴2a=|PF1|+|PF2|=2c•sin75°+2c•sin15°=4csin45°cos30°=
 c
c∴a=
 c
c∴e=
 =
=
故选B.
点评:本题主要考查了椭圆的简单性质.涉及了圆的性质,解三角形问题等.考查了学生综合分析问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
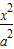 +
+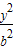 =1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 .
=1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 .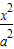 +
+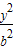 =1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 .
=1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 .