题目内容
设F1(-c,0),F2(c,0)是椭圆
+
=1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| ||
| 3 |
分析:先根据题意和圆的性质可判断出△PF1F2为直角三角形,根据∠PF1F2=5∠PF2F1,推断出∠PF1F2=75°,进而可求得PF1和PF2,利用椭圆的定义求得a和c的关系,则椭圆的离心率可得.
解答:解:由题意△PF1F2为直角三角形,且∠P=90°,∠PF1F2=75°,F1F2=2c,
∴|PF1|=2ccos75°,|PF2|=2ccos15°,
由椭圆的定义知,|PF1|+|PF2|=2c(cos75°+cos15°)=2c
=
c=2a,
∴离心率为e=
=
=
.
故答案为:
∴|PF1|=2ccos75°,|PF2|=2ccos15°,
由椭圆的定义知,|PF1|+|PF2|=2c(cos75°+cos15°)=2c
| (sin15°+cos15°)2 |
| 6 |
∴离心率为e=
| c |
| a |
| c | ||||
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题主要考查了椭圆的简单性质,考查学生的计算能力,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
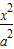 +
+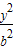 =1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 .
=1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 .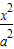 +
+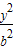 =1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 .
=1(a>b>0)的两个焦点,P是以|F1F2|为直径的圆与椭圆的一个交点,且∠PF1F2=5∠PF2F1,则该椭圆的离心率为 . +
+ =1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为( )
=1(a>b>0)的两个焦点,P是以F1F2为直径的圆与椭圆的一个交点,若∠PF1F2=5∠PF2F1,则椭圆的离心率为( )


