题目内容

（2009•黄冈模拟）平行四边形两条邻边的长分别是4
6
和4
3
，它们的夹角是
π
4
，则平行四边形中较长的对角线的长是
4
15
4
15
．
分析：先利用题中的条件和两个向量的数量积的定义求出
AB
2 ，
AD
2及
AB
•
AD
的值，再根据AC=|
AC
|=
AC
2
=
(
AB
+
AD
)2
 求出AC的值．
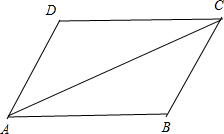
解答：解：如图所示：设平行四边形ABCD中，AB=4
6
，AD=4
3
，∠BAD=
π
4
，则AC为平行四边形中较长的对角线．
由于
AC
=
AB
+
AD
，且
AB
2=96  ， 
AD
2= 48，
AB
•
AD
=4
6
×4
3
cos∠BAD=48．
∴AC=|
AC
|=
AC
2
=
(
AB
+
AD
)2
=
AB
2+
AD
2+2
AB
•
AD
=
96+48+2×48
=
240
=4
15
．
故答案为：4
15
．
点评：本题主要考查两个向量的数量积的定义，向量在几何中的应用，求向量的模的方法，体现了数形结合的数学思想．
练习册系列答案
相关题目
（2009•黄冈模拟）某地正处于地震带上，预计20年后该地将发生地震．当地决定重新选址建设新城区，同时对旧城区进行拆除．已知旧城区的住房总面积为64am2，每年拆除的数量相同；新城区计划用十年建成，第一年建设住房面积2am2，开始几年每年以100%的增长率建设新住房，然后从第五年开始，每年都比上一年减少2am2．
（1）若10年后该地新、旧城区的住房总面积正好比目前翻一番，则每年旧城区拆除的住房面积是多少m2？
（2）设第n（1≤n≤10且n∈N）年新城区的住房总面积为Snm2，求Sn．
（2009•黄冈模拟）如图是一几何体的平面展开图，其中ABCD为正方形，E、F分别为PA、PD的中点．在此几何体中，给出下面四个结论：
①直线BE与直线CF异面；
②直线BE与直线AF异面；
③直线EF∥平面PBC；
④平面BCE⊥平面PAD．
其中正确的命题的个数是
2
2
个．
（2009•黄冈模拟）定义在R上的偶函数y=f（x）满足：
①对x∈R都有f（x+6）=f（x）+f（3）
②f（-5）=-1；
③当x1，x2∈[0，3]且x1≠x2时，都有
f(x1)-f(x2)x1-x2
＞0则
（1）f（2009）=
-1
-1
；
（2）若方程f（x）=0在区间[a，6-a]上恰有3个不同实根，实数a的取值范围是
（-9，-3]
（-9，-3]
．
（2009•黄冈模拟）已知函数f(x)=
1-x2
1+x+x2
(x∈R)．
（Ⅰ）求函数f（x）的单调区间和极值；
（Ⅱ）若（et+2）x2+etx+et-2≥0对满足|x|≤1的任意实数x恒成立，求实数t的取值范围（这里e是自然对数的底数）；
（Ⅲ）求证：对任意正数a、b、λ、μ，恒有f[(
λa+μb
λ+μ
)2]-f(
λa2+μb2
λ+μ
)≥(
λa+μb
λ+μ
)2-
λa2+μb2
λ+μ
．
（2009•黄冈模拟）四个大小相同的小球分别标有数字1、1、2、2，把它们放在一个盒子里，从中任意摸出两个小球，它们所标有的数字分别为x，y，记ξ=x+y．
（1）求随机变量ξ的分布列及数学期望；
（2）设“函数f（x）=x2-ξx-1在区间（2，3）上有且只有一个零点”为事件A，求事件A发生的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网