题目内容
已知离心率为 的椭圆的中心在原点,焦点在x轴上,双曲线以椭圆的长轴为实轴,短轴为虚轴,且焦距为2
的椭圆的中心在原点,焦点在x轴上,双曲线以椭圆的长轴为实轴,短轴为虚轴,且焦距为2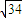 .
.(I)求椭圆及双曲线的方程;
(Ⅱ)设椭圆的左、右顶点分别为A,B,在第二象限内取双曲线上一点P,连结BP交椭圆于点M,连结PA并延长交椭圆于点N,若
 =
= .求四边形ANBM的面积.
.求四边形ANBM的面积.
【答案】分析:(Ⅰ)设出椭圆方程和双曲线方程,由椭圆的离心率是 ,双曲线的焦距为2
,双曲线的焦距为2 联立方程组求出a和b的值,则椭圆及双曲线的方程可求;
联立方程组求出a和b的值,则椭圆及双曲线的方程可求;
(Ⅱ)由(Ⅰ)中求出的椭圆方程求出A和B的坐标,设出M点的坐标,由 得M为BP的中点,从而求出P点坐标,把M的坐标代入椭圆方程,把P的坐标代入双曲线方程,联立后求出M和P的具体值,然后把四边形ANBM的面积转化为三角形ANB的面积求解.
得M为BP的中点,从而求出P点坐标,把M的坐标代入椭圆方程,把P的坐标代入双曲线方程,联立后求出M和P的具体值,然后把四边形ANBM的面积转化为三角形ANB的面积求解.
解答:解:(I)设椭圆方程为 (a>b>0).
(a>b>0).
则根据题意,双曲线的方程为
 ,且满足
,且满足
 ,解方程组得
,解方程组得
∴椭圆的方程为 ,双曲线的方程
,双曲线的方程 ;
;
(Ⅱ)由(I)得A(-5,0),B(5,0),|AB|=10.
设M(x,y),则由 得M为BP的中点,所以P点坐标为(2x-5,2y),
得M为BP的中点,所以P点坐标为(2x-5,2y),
将M、P坐标代入椭圆和双曲线方程,得
 ,
,
消去y,得
解之得 或x=5(舍)
或x=5(舍)
所以 ,由此可得
,由此可得 ,
,
所以 .
.
当P为 时,直线PA的方程是
时,直线PA的方程是
即 .
.
代入 ,得2x2+15x+25=0
,得2x2+15x+25=0
所以 或-5(舍),
或-5(舍),
所以 ,xN=xM,MN⊥x轴.
,xN=xM,MN⊥x轴.
所以 .
.
点评:本题主要考查了圆锥曲线的方程,直线与圆锥曲线的位置关系的应用,考查了数学转化思想方法,直线与圆锥曲线问题的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.
 ,双曲线的焦距为2
,双曲线的焦距为2 联立方程组求出a和b的值,则椭圆及双曲线的方程可求;
联立方程组求出a和b的值,则椭圆及双曲线的方程可求;(Ⅱ)由(Ⅰ)中求出的椭圆方程求出A和B的坐标,设出M点的坐标,由
 得M为BP的中点,从而求出P点坐标,把M的坐标代入椭圆方程,把P的坐标代入双曲线方程,联立后求出M和P的具体值,然后把四边形ANBM的面积转化为三角形ANB的面积求解.
得M为BP的中点,从而求出P点坐标,把M的坐标代入椭圆方程,把P的坐标代入双曲线方程,联立后求出M和P的具体值,然后把四边形ANBM的面积转化为三角形ANB的面积求解.解答:解:(I)设椭圆方程为
 (a>b>0).
(a>b>0).则根据题意,双曲线的方程为
 ,且满足
,且满足 ,解方程组得
,解方程组得
∴椭圆的方程为
 ,双曲线的方程
,双曲线的方程 ;
;(Ⅱ)由(I)得A(-5,0),B(5,0),|AB|=10.
设M(x,y),则由
 得M为BP的中点,所以P点坐标为(2x-5,2y),
得M为BP的中点,所以P点坐标为(2x-5,2y),将M、P坐标代入椭圆和双曲线方程,得
 ,
,消去y,得

解之得
 或x=5(舍)
或x=5(舍)所以
 ,由此可得
,由此可得 ,
,所以
 .
.当P为
 时,直线PA的方程是
时,直线PA的方程是
即
 .
.代入
 ,得2x2+15x+25=0
,得2x2+15x+25=0所以
 或-5(舍),
或-5(舍),所以
 ,xN=xM,MN⊥x轴.
,xN=xM,MN⊥x轴.所以
 .
.点评:本题主要考查了圆锥曲线的方程,直线与圆锥曲线的位置关系的应用,考查了数学转化思想方法,直线与圆锥曲线问题的特点是计算量比较大,要求考生具备较强的运算推理的能力,是难题.

练习册系列答案
相关题目
 . 已知离心率为
. 已知离心率为 的椭圆
的椭圆 上的点到
上的点到 的最长距离为
的最长距离为
 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点
 的椭圆C的中心在坐标原点O,一焦点坐标为(1,0),圆O的方程为x2+y2=7.
的椭圆C的中心在坐标原点O,一焦点坐标为(1,0),圆O的方程为x2+y2=7.
 的椭圆
的椭圆 的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆的两条切线分别交y轴于M、N两点.
的右焦点F是圆(x-1)2+y2=1的圆心,过椭圆上的动点P作圆的两条切线分别交y轴于M、N两点.
 的椭圆
的椭圆 上的点到左焦点
上的点到左焦点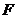 的最长距离为
的最长距离为
 ,若点
,若点 在
在 轴上,且使得
轴上,且使得 为
为 的一条内角平分线,则称点
的一条内角平分线,则称点