题目内容
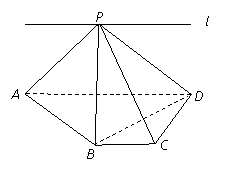
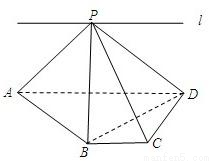
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.(1)求证:PA⊥BD;
(2)若PC与CD不垂直,求证:PA≠PD;
(3)若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,使得直线PC∥平面EBD.
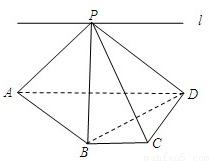
【答案】分析:(1)要证PA⊥BD,只需证明AB⊥BD、PB⊥BD(因为PA、PB是平面PAB内的两条相交直线);
(2)利用反证法证明,推出CD⊥PC,与已知条件PC与CD不垂直矛盾,可证:PA≠PD;
(3)在上l取一点E,使PE=BC,利用直线l∥直线BC,推出PC∥BE,可以证明直线PC∥平面EBD.
解答: (1)∵ABCD为直角梯形,AD=
(1)∵ABCD为直角梯形,AD= AB=
AB= BD,
BD,
∴AB⊥BD,(1分)
PB⊥BD,AB∩PB=B,AB,PB?平面PAB,
BD⊥平面PAB,(4分)
PA?面PAB,∴PA⊥BD.(5分)
(2)假设PA=PD,取AD中点N,连PN,BN,
则PN⊥AD,BN⊥AD,(7分)
AD⊥平面PNB,得PB⊥AD,(8分)
又PB⊥BD,得PB⊥平面ABCD,
∴PB⊥CD(9分)
又∵BC⊥CD,∴CD⊥平面PBC,
∴CD⊥PC,与已知条件PC与CD
不垂直矛盾
∴PC≠PD(10分)
(3)在上l取一点E,使PE=BC,(11分)
∵PE∥BC,∴四边形BCPE是平行四边形,(12分)
∴PC∥BE,PC?平面EBD,BE?平面EBD
∴PC∥平面EBD.(14分)
点评:本题考查直线与直线垂直,直线与平面平行,异面直线所成的角,考查空间想象能力,是中档题.
(2)利用反证法证明,推出CD⊥PC,与已知条件PC与CD不垂直矛盾,可证:PA≠PD;
(3)在上l取一点E,使PE=BC,利用直线l∥直线BC,推出PC∥BE,可以证明直线PC∥平面EBD.
解答:
 (1)∵ABCD为直角梯形,AD=
(1)∵ABCD为直角梯形,AD= AB=
AB= BD,
BD,∴AB⊥BD,(1分)
PB⊥BD,AB∩PB=B,AB,PB?平面PAB,
BD⊥平面PAB,(4分)
PA?面PAB,∴PA⊥BD.(5分)
(2)假设PA=PD,取AD中点N,连PN,BN,
则PN⊥AD,BN⊥AD,(7分)
AD⊥平面PNB,得PB⊥AD,(8分)
又PB⊥BD,得PB⊥平面ABCD,
∴PB⊥CD(9分)
又∵BC⊥CD,∴CD⊥平面PBC,
∴CD⊥PC,与已知条件PC与CD
不垂直矛盾
∴PC≠PD(10分)
(3)在上l取一点E,使PE=BC,(11分)
∵PE∥BC,∴四边形BCPE是平行四边形,(12分)
∴PC∥BE,PC?平面EBD,BE?平面EBD
∴PC∥平面EBD.(14分)
点评:本题考查直线与直线垂直,直线与平面平行,异面直线所成的角,考查空间想象能力,是中档题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
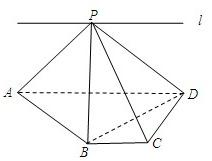 如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.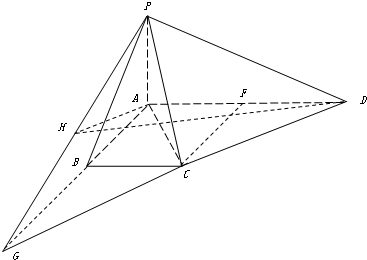 如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.
如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.