题目内容
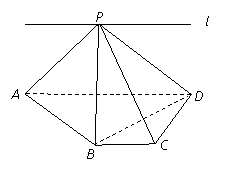
 如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.
如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.(1)求点P到CD的距离;
(2)求证:平面PAC⊥平面PCD;
(3)求平面PAB与平面PCD所成二面角的大小.
分析:方法一:
(1)借助于三垂线定理先照出或作出垂线段,由已知,PA⊥平面ABCD,考虑是否AC⊥CD.可以证出AC⊥CD,所以P到CD的距离为PC.
(2)要证平面PAC⊥平面PCD;可通过证明CD⊥平面PAC而证得.
(3)延长DC交AB的延长线于G,连结PG.易证DA⊥平面PAB,
过A作AH⊥PG,垂足为H,连结DH,得到∠AHD为所求二面角的平面角.
方法二
(1)以A为原点建立空间直角坐标系,表示出相关点的坐标,通过
•
=-1+1=0得出PC⊥CD
即P到CD的距离为|
|.
(2)要证平面PAC⊥平面PCD;可通过证明CD⊥平面PAC而证得.
(3)分别求得平面PAB与平面PCD的一个法向量,通过两法向量夹角求出平面PAB与平面PCD所成二面角的大小
(1)借助于三垂线定理先照出或作出垂线段,由已知,PA⊥平面ABCD,考虑是否AC⊥CD.可以证出AC⊥CD,所以P到CD的距离为PC.
(2)要证平面PAC⊥平面PCD;可通过证明CD⊥平面PAC而证得.
(3)延长DC交AB的延长线于G,连结PG.易证DA⊥平面PAB,
过A作AH⊥PG,垂足为H,连结DH,得到∠AHD为所求二面角的平面角.
方法二
(1)以A为原点建立空间直角坐标系,表示出相关点的坐标,通过
| PC |
| CD |
即P到CD的距离为|
| PC |
(2)要证平面PAC⊥平面PCD;可通过证明CD⊥平面PAC而证得.
(3)分别求得平面PAB与平面PCD的一个法向量,通过两法向量夹角求出平面PAB与平面PCD所成二面角的大小
解答:解:(方法一)
(1)、取AD的中点F,连结CF.
易证四边形ABCF是正方形,
∴CF=AB=1又∵AD=2
∴CF=
AD∴∠ACD=90°
即AC⊥CD,∵PA⊥平面ABCD,∴PC⊥CD,
∴P到CD的距离为PC,PC=
.
(2)∵AC⊥CD,PC⊥CD且AC∩PC=C,
∴CD⊥平面PAC.
又∵CD⊆平面PCD,
∴平面PAC⊥平面PCD.
(3)延长DC交AB的延长线于G,连结PG.
∴平面PAB∩平面PCD=PG,
易证DA⊥平面PAB.
过A作AH⊥PG,垂足为H,连结DH,
得到∠AHD为所求二面角的平面角.AH=
,tan∠AHD=
=
,
∴∠AHD=arctan
.
∴平面PAB与平面PCD所成二面角为arctan
.
(方法二)
(1)建立如图所示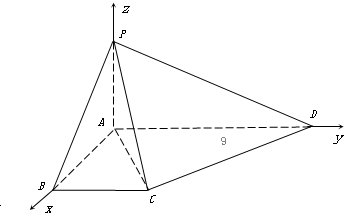 的空间直角坐标系
的空间直角坐标系
得到D(0,2,0),P(0,0,1),B(1,0,0),C(1,1,0)
=(1,1,-1),
=(-1,1,0).
∴
•
=-1+1=0,∴PC⊥CD.
即P到CD的距离为|
|,
∴|
|=
(2)∵PA⊥平面ABCD,∴PA⊥CD.
又∵PC⊥CD,PC∩PA=P,∴CD⊥平面PAC.
又CD⊆平面PCD,∴平面PAC⊥平面PCD.
(3)平面PAB的一个法向量为
=(0,2,0).
设
=(c,a,b)为平面PCD的法向量,则
•
=0,
•
=0.
得到
,解得
.
不妨设c=1,∴
=(1,1,2)cos<
,
>=
=
=
.
∴平面PAB与平面PCD所成二面角的大小为arccos
.
(1)、取AD的中点F,连结CF.
易证四边形ABCF是正方形,
∴CF=AB=1又∵AD=2
∴CF=
| 1 |
| 2 |
即AC⊥CD,∵PA⊥平面ABCD,∴PC⊥CD,
∴P到CD的距离为PC,PC=
| 3 |
(2)∵AC⊥CD,PC⊥CD且AC∩PC=C,
∴CD⊥平面PAC.
又∵CD⊆平面PCD,
∴平面PAC⊥平面PCD.
(3)延长DC交AB的延长线于G,连结PG.
∴平面PAB∩平面PCD=PG,
易证DA⊥平面PAB.
过A作AH⊥PG,垂足为H,连结DH,
得到∠AHD为所求二面角的平面角.AH=
| 2 |
| 5 |
| 5 |
| AD |
| AH |
| 5 |
∴∠AHD=arctan
| 5 |
∴平面PAB与平面PCD所成二面角为arctan
| 5 |
(方法二)
(1)建立如图所示
 的空间直角坐标系
的空间直角坐标系得到D(0,2,0),P(0,0,1),B(1,0,0),C(1,1,0)
| PC |
| CD |
∴
| PC |
| CD |
即P到CD的距离为|
| PC |
∴|
| PC |
| 3 |
(2)∵PA⊥平面ABCD,∴PA⊥CD.
又∵PC⊥CD,PC∩PA=P,∴CD⊥平面PAC.
又CD⊆平面PCD,∴平面PAC⊥平面PCD.
(3)平面PAB的一个法向量为
| AD |
设
| n |
| n |
| PC |
| n |
| CD |
得到
|
|
不妨设c=1,∴
| n |
| AD |
| n |
| ||||
|
|
| 2 | ||
2×
|
| ||
| 6 |
∴平面PAB与平面PCD所成二面角的大小为arccos
| ||
| 6 |
点评:本题考查空间直线、平面位置关系的判断,二面角大小求解,考查空间想象能力、推理论证、计算、转化能力.利用向量这一工具,解决空间几何体问题,能够降低思维难度.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.