题目内容
已知f(x)=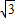 sin(2x-
sin(2x-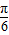 )+2sin2(x-
)+2sin2(x-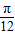 ),x∈R
),x∈R(1)求f(x)的最小正周期及单调增区间
(2)f(x)可由y=sinx作怎样的变换得到?
【答案】分析:(1)利用二倍角、辅助角公式,化简函数,从而可求f(x)的最小正周期及单调增区间;
(2)利用三角函数的图象变换规律,可得结论.
解答:解:(1)f(x)=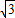 sin(2x-
sin(2x-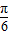 )+2sin2(x-
)+2sin2(x-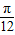 )=
)=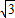 sin(2x-
sin(2x-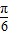 )+1-cos(2x-
)+1-cos(2x-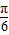 )=2sin(
)=2sin(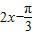 )+1,
)+1,
∴T=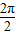 =π
=π
由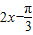 ∈
∈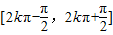 得增区间为
得增区间为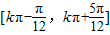 (k∈Z);
(k∈Z);
(2)y=sinx右移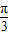 得到y=sin(x-
得到y=sin(x-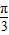 ),纵不变,横变为原来
),纵不变,横变为原来 ,得到y=sin(
,得到y=sin(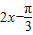 ),横不变,纵变为2倍得到y=2sin(
),横不变,纵变为2倍得到y=2sin(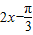 ),上移1个单位即得y=2sin(
),上移1个单位即得y=2sin( )+1.
)+1.
点评:本题考查三角函数的化简,考查三角函数的性质,考查学生分析解决问题的能力,属于中档题.
(2)利用三角函数的图象变换规律,可得结论.
解答:解:(1)f(x)=
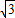 sin(2x-
sin(2x-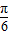 )+2sin2(x-
)+2sin2(x-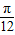 )=
)=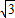 sin(2x-
sin(2x-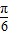 )+1-cos(2x-
)+1-cos(2x-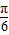 )=2sin(
)=2sin(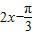 )+1,
)+1,∴T=
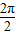 =π
=π由
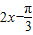 ∈
∈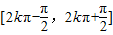 得增区间为
得增区间为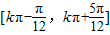 (k∈Z);
(k∈Z);(2)y=sinx右移
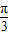 得到y=sin(x-
得到y=sin(x-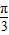 ),纵不变,横变为原来
),纵不变,横变为原来 ,得到y=sin(
,得到y=sin(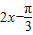 ),横不变,纵变为2倍得到y=2sin(
),横不变,纵变为2倍得到y=2sin(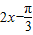 ),上移1个单位即得y=2sin(
),上移1个单位即得y=2sin( )+1.
)+1.点评:本题考查三角函数的化简,考查三角函数的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
已知f(x)=sin(x+
),g(x)=cos(x-
),则f(x)的图象( )
| π |
| 2 |
| π |
| 2 |
| A、与g(x)的图象相同 | ||
| B、与g(x)的图象关于y轴对称 | ||
C、向左平移
| ||
D、向右平移
|