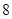题目内容
已知
、
之间的一组数据如右表：
| 0 | 1 | 2 | 3 |
| 8 | 2 | 6 | 4 |
所表示的直线必经过点 ( )A．（0，0） B．（1.5,5） C．（4,1.5） D．（2,2）
B
解析试题分析：根据题意可知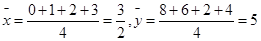
，那么可知线性回归方程所表示的直线必经过点样本的中心点
，那么可知结论为B
考点：回归直线的性质
点评：本题考查平均值的计算方法，回归直线的性质：回归直线方程一定过样本的中心点
练习册系列答案
相关题目
S大学艺术系表演专业的报考人数连创新高，2010年报名刚结束，某考生想知道这次报考该专业的人数．已知该专业考生的考号是按0001,0002，…的顺序从小到大依次排列的，他随机了解了50名考生的考号，经计算，这50个考号的和是25025， 估计2010年报考S大学艺术系表演专业的考生大约有( )
| A．500人 | B．1000人 | C．1500人 | D．2000人 |
下图是2013赛季詹姆斯(甲）、安东尼（乙）两名篮球运动员连续参
加的7场比赛得分的 情况，如茎叶图表示，则甲乙两名运动员的中位数分别为（ ）
| 甲 | | 乙 | ||||
| 5 | 7 | 9 | 1 | 1 | 1 | 3 |
| 3 | 4 | 6 | 2 | 2 | 0 | |
| | | 2 | 3 | 1 | 0 | |
A．23、22 B．19、20 C．26、22 D．23、20
为了解一片速生林的生长情况，随机测量了其中100株树木的 底部周长（单位：cm）．根据所得数据画出了样本的频率分布直方图，那么在这100株树木中，底部周长小于110cm的株数是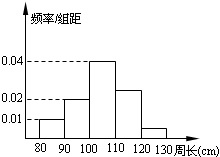
| A．80 | B．70 | C．60 | D．30 |
下列关于由最小二乘法求出的回归直线方程
=2－x的说法中，不正确的是
| A．变量x与y正相关 |
B．该回归直线必过样本点中心（ ） |
| C．当x=l时，y的预报值为l |
D．当残差平方和 越小时模型拟合的效果越好 |
某大学中文系共有本科生5000人，其中一、二、三、四年级的学生比为5：4：3：1，要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本，则应抽二年级的学生（ ）
| A．100人 | B．80人 | C．60人 | D．20人 |
为了评价某个电视栏目的改革效果，在改革前后分别从某居民点抽取了1000位居民进行调查，经过计算得K2
4．358，根据这一数据分析，下列说法正确的是（ ）
| A．有95％的人认为该栏日优秀 |
| B．有95％的人认为该栏目是否优秀与改革有关系 |
| C．有95％的把握认为电视栏目是否优秀与改革有关系 |
| D．没有理由认为电视栏目是否优秀与改革有关系 |
的值为（ ）
在两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟和效果最好的模型是（ ）
| A．模型1的相关指数R2为0.25 | B．模型2的相关指数R2为0.50 |
| C．模型3的相关指数R2为0.98 | D．模型4的相关指数R2为0.80 |