题目内容
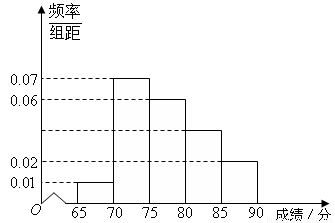
某中学作为蓝色海洋教育特色学校,随机抽取100名学生,进行一次海洋知识测试,按测试成绩分组如下:第一组[65,70),第二组[70,75),第三组[75,80),第四组[80,85),第五组[85,90)(假设考试成绩均在[65,90)内),得到频率分布直方图如图:
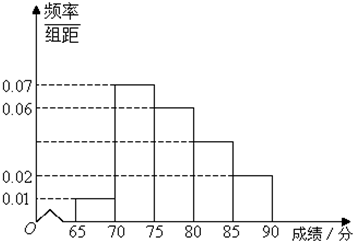
(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的概率.

(1)求测试成绩在[80,85)内的频率;
(2)从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋知识宣讲小组,定期在校内进行义务宣讲,并在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,求第四组至少有一名同学被抽中的概率.
分析:(1)设测试成绩在[80,85)内的频率为x,根据所有直方图的面积之和等于1求得 x的值.
(2)先求得抽取的这6名同学中,第三、四、五组同学的数量分别为3,2,1.在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,所有
的抽法共有
种,而第四组至少有一名同学被抽中的抽法有
•
+
=9种,由此求得第四组至少有一名同学被抽中的概率.
(2)先求得抽取的这6名同学中,第三、四、五组同学的数量分别为3,2,1.在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,所有
的抽法共有
| C | 2 6 |
| C | 1 2 |
| C | 1 4 |
| C | 2 2 |
解答:解:(1)设测试成绩在[80,85)内的频率为x,根据所给的频率分布直方图可得,
0.01×5+0.07×5+0.06×5+5x+0.02×5=1,解得 x=0.04.
(2)第三、四、五组同学的数量之比为 0.3:0.2:0.1=3:2:1,
故抽取的这6名同学中,第三、四、五组同学的数量分别为3,2,1.
在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,所有的抽法共有
=15种,
而第四组至少有一名同学被抽中的抽法有
•
+
=9种,
第四组至少有一名同学被抽中的概率为
=
.
0.01×5+0.07×5+0.06×5+5x+0.02×5=1,解得 x=0.04.
(2)第三、四、五组同学的数量之比为 0.3:0.2:0.1=3:2:1,
故抽取的这6名同学中,第三、四、五组同学的数量分别为3,2,1.
在这6名同学中随机选取2名参加市组织的蓝色海洋教育义务宣讲队,所有的抽法共有
| C | 2 6 |
而第四组至少有一名同学被抽中的抽法有
| C | 1 2 |
| C | 1 4 |
| C | 2 2 |
第四组至少有一名同学被抽中的概率为
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题主要考查频率分步直方图的性质,分层抽样的定义和方法,古典概率及其计算公式,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
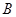 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是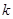 ,那么二项式
,那么二项式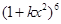 的展开式中
的展开式中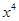 的系数为
的系数为 中至少有一个被选中的不同选法种数是
中至少有一个被选中的不同选法种数是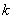 ,那么二项式
,那么二项式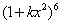 的展开式中
的展开式中 的系数为
的系数为