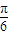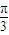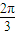题目内容
已知函数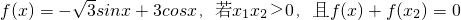 ,则|x1+x2|的最小值为
,则|x1+x2|的最小值为
- A.

- B.

- C.

- D.

D
分析:题干错误:x1•x2>0,且f(x)+f(x2)=0,应该 x1•x2>0,且f(x1)+f(x2)=0.
利用三角函数的恒等变换化简函数f(x)的解析式为=-2 sin(x-
sin(x- ),由题意可得|x1+x2|的最小值等于函数f(x)的绝对值最小的零点的2倍,求出函数f(x)的绝对值最小的零点,
),由题意可得|x1+x2|的最小值等于函数f(x)的绝对值最小的零点的2倍,求出函数f(x)的绝对值最小的零点,
即可求得结果.
解答:∵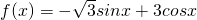 =2
=2 (-
(- sinx+
sinx+ cosx)=2
cosx)=2 sin(
sin( -x)=-2
-x)=-2 sin(x-
sin(x- ),x1•x2>0,且f(x1)+f(x2)=0,
),x1•x2>0,且f(x1)+f(x2)=0,
∴x1+x2 等于函数的零点的2倍,∴|x1+x2|的最小值等于函数f(x)的绝对值最小的零点的2倍.
∴令-2 sin(x-
sin(x- )=0 可得sin(x-
)=0 可得sin(x- )=0,x-
)=0,x- =kπ,k∈z.故函数f(x)的绝对值最小的零点为
=kπ,k∈z.故函数f(x)的绝对值最小的零点为 ,故|x1+x2|的最小值为
,故|x1+x2|的最小值为 ,
,
故选D.
点评:本题主要考查三角函数的恒等变换及化简求值,求函数的零点,体现了转化的数学思想,属于中档题.
分析:题干错误:x1•x2>0,且f(x)+f(x2)=0,应该 x1•x2>0,且f(x1)+f(x2)=0.
利用三角函数的恒等变换化简函数f(x)的解析式为=-2
 sin(x-
sin(x- ),由题意可得|x1+x2|的最小值等于函数f(x)的绝对值最小的零点的2倍,求出函数f(x)的绝对值最小的零点,
),由题意可得|x1+x2|的最小值等于函数f(x)的绝对值最小的零点的2倍,求出函数f(x)的绝对值最小的零点,即可求得结果.
解答:∵
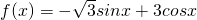 =2
=2 (-
(- sinx+
sinx+ cosx)=2
cosx)=2 sin(
sin( -x)=-2
-x)=-2 sin(x-
sin(x- ),x1•x2>0,且f(x1)+f(x2)=0,
),x1•x2>0,且f(x1)+f(x2)=0,∴x1+x2 等于函数的零点的2倍,∴|x1+x2|的最小值等于函数f(x)的绝对值最小的零点的2倍.
∴令-2
 sin(x-
sin(x- )=0 可得sin(x-
)=0 可得sin(x- )=0,x-
)=0,x- =kπ,k∈z.故函数f(x)的绝对值最小的零点为
=kπ,k∈z.故函数f(x)的绝对值最小的零点为 ,故|x1+x2|的最小值为
,故|x1+x2|的最小值为 ,
,故选D.
点评:本题主要考查三角函数的恒等变换及化简求值,求函数的零点,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
(x∈R)时,则下列结论不正确的是( )
| x |
| 1+|x| |
| A、?x∈R,等式f(-x)+f(x)=0恒成立 |
| B、?m∈(0,1),使得方程|f(x)|=m有两个不等实数根 |
| C、?x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2) |
| D、?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点 |
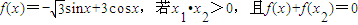 ,则|x1+x2|的最小值为( )
,则|x1+x2|的最小值为( )
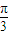

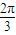
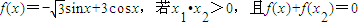 ,则|x1+x2|的最小值为( )
,则|x1+x2|的最小值为( )