题目内容
已知p:对任意m∈[﹣1,1],不等式![]() 恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.
恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.
考点:
命题的真假判断与应用;复合命题的真假.
专题:
计算题.
分析:
分别求出命题p和q中m的范围和a的范围,若“p或q”为真,“p且q”为假,可知命题p与q一真一假,从而求出a的取值范围;
解答:
解:若p成立,由m∈[﹣1,1]得![]() ,
,
即a2﹣5a﹣3≥3,解得a≥6或a≤﹣1;
若q成立,则不等式中△>0,解得![]() 或
或![]() ;
;
若“p或q”为真,“p且q”为假,则命题p与q一真一假,
(1)若p真q假,则![]() ;
;
(2)若p假q真,则![]() ;
;
综上:a的取值范围是![]() 或
或![]()
点评:
此题主要命题的真假的判断与应用以及复合命题的真假,是一道基础题,计算量有些大;

练习册系列答案
相关题目
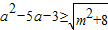 恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.
恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.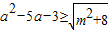 恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.
恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.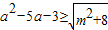 恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.
恒成立;q:存在x,使不等式x2+ax+2<0成立,若“p或q”为真,“p且q”为假,求a的取值范围.