题目内容
已知双曲线9y2-m2x2=1（m＞0）的一个顶点到它的一条渐近线的距离为
，则m= ．
【答案】分析：先根据双曲线方程求得a和b，进而可得渐近线方程和定点坐标，根据定点到渐近线的距离等于
，进而求得m．
解答：解：根据双曲线方程可知a=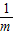
，b=
所以渐近线y=±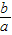
x=±
x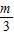
取正
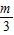x-y=0
顶点（0，
）
则距离=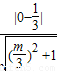
=
解得m2=16
∴m=4
故答案为4
点评：本题主要考查了双曲线的简单性质．属基础题．
，进而求得m．解答：解：根据双曲线方程可知a=
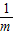，b=所以渐近线y=±
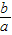x=±x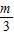取正
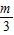x-y=0顶点（0，
）则距离=
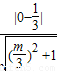=解得m2=16
∴m=4
故答案为4
点评：本题主要考查了双曲线的简单性质．属基础题．
练习册系列答案
相关题目
已知双曲线9y2-m2x2=1（m＞0）的一个顶点到它的一条渐近线的距离为
，则m=（ ）
| 1 |
| 5 |
| A、1 | B、2 | C、3 | D、4 |
，则m=
，则m=