题目内容
数列{an}满足:a1=1,an+1= 。
。
(1)求a2,a3;
(2)设bn=a2n-2,n∈N*,求证:数列{bn}是等比数列,并求其通项公式;
(3)已知cn= |bn|,求证:
|bn|,求证: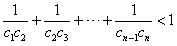 。
。
 。
。(1)求a2,a3;
(2)设bn=a2n-2,n∈N*,求证:数列{bn}是等比数列,并求其通项公式;
(3)已知cn=
 |bn|,求证:
|bn|,求证: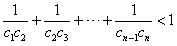 。
。解:(1)由数列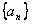 的递推关系易知:
的递推关系易知:
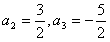 ;
;
(2)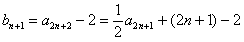
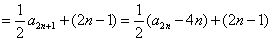
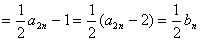
又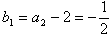
∴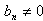
∴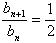
即数列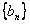 是公比为
是公比为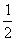 ,首项为-
,首项为-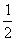 的等比数列
的等比数列
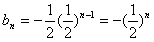 ;
;
(3)由(2)有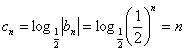
∵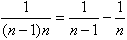
∴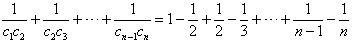
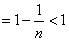 。
。
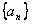 的递推关系易知:
的递推关系易知: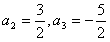 ;
;(2)
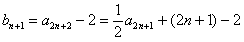
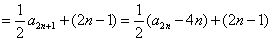
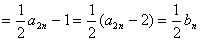
又
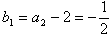
∴
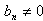
∴
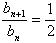
即数列
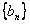 是公比为
是公比为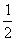 ,首项为-
,首项为-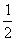 的等比数列
的等比数列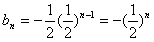 ;
;(3)由(2)有
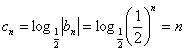
∵
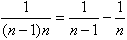
∴
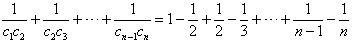
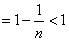 。
。
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目