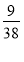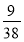Question

为了解某班学生喜爱打篮球是否与性别有关，对本班48人进行了问卷调查得到了如下的2×2列联表：

	喜爱打篮球	不喜爱打篮球	合计
男生		6
女生	10
合计			48

已知在全班48人中随机抽取1人，抽到喜爱打篮球的学生的概率为.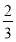

(1)请将上面的2×2列联表补充完整(不用写计算过程)；

(2)你是否有95%的把握认为喜爱打篮球与性别有关？说明你的理由；

(3)现从女生中抽取2人进一步调查，设其中喜爱打篮球的女生人数为X，求X的分布列与数学期望．

下面的临界值表供参考：

P(χ2≥x0)或 P(K2≥k0)	0.10	0.05	0.010	0.005
x0(或k0)	2.706	3.841	6.635	7.879

 

(参考公式)χ2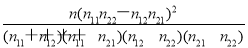＝，其中n＝n11＋n12＋n21＋n22或K2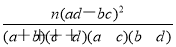＝，其中n＝a＋b＋c＋d)

 

Answer 1

(1)

	喜爱打篮球	不喜爱打篮球	合计
男生	22	6	28
女生	10	10	20
合计	32	16	48

(2)有95%的把握认为喜爱打篮球与性别有关(3) 1

【解析】(1)列联表补充如下：

	喜爱打篮球	不喜爱打篮球	合计
男生	22	6	28
女生	10	10	20
合计	32	16	48

(2)由K2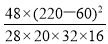＝≈4.286.

因为4.286>3.841，所以，有95%的把握认为喜爱打篮球与性别有关．

(3)喜爱打篮球的女生人数X的可能取值为0,1,2.

其概率分别为P(X＝0)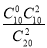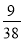＝＝，P(X＝1)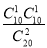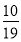＝＝，P(X＝2)＝＝，

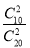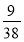故X的分布列为

X	0	1	2
P

X的数学期望为E(X)＝0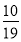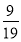＋＋＝1.