题目内容
不等式2x2-x-1>0的解集是
A. | B.(1, + ) ) |
C.(- ,1)∪(2,+ ,1)∪(2,+ ) ) | D. |
D
解析试题分析:把不等式的左边分解因式后,根据两数相乘同号得正的取符号法则,得到2x+1与x-1同号,可化为两个不等式组,分别求出两不等式组的解集的并集即可得到原不等式的解集。解:不等式2x2-x-1>0,因式分解得:(2x+1)(x-1)>0,则根据二次函数图像来得到使得函数值大于零的变量的取值范围是 ,选D.
,选D.
考点:一元二次不等式的解法
点评:此题考查了一元二次不等式的解法,利用了转化的思想,是高考中常考的基本题型.把一元二次不等式转化为两个不等式组的理论依据为:两数相乘同号得正、异号得负的取符号法则

练习册系列答案
相关题目
设a>0,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
设 ,
, ,
, (其中
(其中 为自然对数的底数),则
为自然对数的底数),则
A. | B. | C.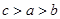 | D. |
已知函数 若存在
若存在 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
若函数 在区间
在区间 上的最大值是最小值的
上的最大值是最小值的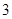 倍,则
倍,则 的值为( )
的值为( )
A. | B. | C. | D. |
 为奇函数,且函数
为奇函数,且函数 的图像关于点
的图像关于点 对称,点
对称,点 在直线
在直线 ,则
,则 的最小值是( )
的最小值是( )



 的x取值范围是 ( )
的x取值范围是 ( )




 ,则
,则 ( )
( ) C.-4 D-
C.-4 D-