题目内容
直线l与抛物线y2=4x交于两点A、B,O为原点,且| OA |
| OB |
(1)求证:直线l恒过一定点;
(2)若4
| 6 |
| 30 |
(3)设抛物线的焦点为F,∠AFB=θ,试问θ角能否等于120°?若能,求出相应的直线l的方程;若不能,请说明理由.
分析:(1)若直线l与x轴不垂直,设其方程为y=kx+b,l与抛物线y2=4x的交点坐标分别为A(x1,y1)、B(x2,y2),根据
•
=-4求得y1y2,把直线与抛物线方程方程联立消去x根据韦达定理求得y1y2的表达式进而可求得b和k的关系,整理直线方程可知直线l过定点(2,0);若直线l⊥x轴,易得x1=x2=2,则l也过定点(2,0).
(2)由(1)可求得|AB|2的表达式,从而根据4
≤|AB|≤4
求得k的范围.
(3)假定θ=
p,则可得cosθ,根据抛物线定义得|AF|=x1+1,|BF|=x2+1.从而表示出|AF|2+|BF|2-|AB|2和|AF|•|BF|代入
=-
整理得x1+x2+1=0与x1>0且x2>0相矛盾,经检验,当AB⊥x轴时,θ=2arctan2
>
p.综合可知,θ≠
p.
| OA |
| OB |
(2)由(1)可求得|AB|2的表达式,从而根据4
| 6 |
| 30 |
(3)假定θ=
| 2 |
| 3 |
| |AF|2+|BF|2-|AB|2 |
| 2|AF|•|BF| |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
解答: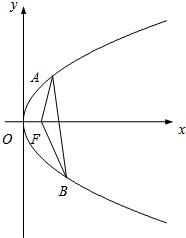 解:(1)1°若直线l与x轴不垂直,设其方程为y=kx+b,
解:(1)1°若直线l与x轴不垂直,设其方程为y=kx+b,
l与抛物线y2=4x的交点坐标分别为A(x1,y1)、B(x2,y2),
由
•
=-4得x1x2+y1y2=-4,即
+y1y2=-4,
则y1y2=-8.
又由
得ky2-4y+4b=0(k≠0).
则y1y2=
=-8,即b=-2k,
则直线l的方程为y=k(x-2),则直线l过定点(2,0).
2°若直线l⊥x轴,易得x1=x2=2,则l也过定点(2,0).
综上,直线l恒过定点(2,0).
(2)由(I)得|AB|2=(1+
)(y2-y1)2=
(
+32)
从而6≤
(
+2)≤30.
解得k∈[-1,-
]∪[
,1].
(3)假定θ=
p,则有cosθ=-
,
如图,即
=-
(*)
由(1)得y1y2=-8,x1x2=
=4.
由定义得|AF|=x1+1,|BF|=x2+1.
从而有|AF|2+|BF|2-|AB|2=(x1+1)2+(x2+1)2-(x1-x2)2-(y1-y2)2=-2(x1+x2)-6,
|AF|•|BF|=(x1+1)(x2+1)=x1x2+x1+x2+1=x1+x2+5
将代入(*)得
=-
,即x1+x2+1=0.
这与x1>0且x2>0相矛盾!
经检验,当AB⊥x轴时,θ=2arctan2
>
p.
综上,θ≠
p.
 解:(1)1°若直线l与x轴不垂直,设其方程为y=kx+b,
解:(1)1°若直线l与x轴不垂直,设其方程为y=kx+b,l与抛物线y2=4x的交点坐标分别为A(x1,y1)、B(x2,y2),
由
| OA |
| OB |
| ||||
| 16 |
则y1y2=-8.
又由
|
则y1y2=
| 4b |
| k |
则直线l的方程为y=k(x-2),则直线l过定点(2,0).
2°若直线l⊥x轴,易得x1=x2=2,则l也过定点(2,0).
综上,直线l恒过定点(2,0).
(2)由(I)得|AB|2=(1+
| 1 |
| k2 |
| 1+k2 |
| k2 |
| 16 |
| k2 |
从而6≤
| 1+k2 |
| k2 |
| 1 |
| k2 |
解得k∈[-1,-
| 1 |
| 2 |
| 1 |
| 2 |
(3)假定θ=
| 2 |
| 3 |
| 1 |
| 2 |
如图,即
| |AF|2+|BF|2-|AB|2 |
| 2|AF|•|BF| |
| 1 |
| 2 |
由(1)得y1y2=-8,x1x2=
| ||||
| 16 |
由定义得|AF|=x1+1,|BF|=x2+1.
从而有|AF|2+|BF|2-|AB|2=(x1+1)2+(x2+1)2-(x1-x2)2-(y1-y2)2=-2(x1+x2)-6,
|AF|•|BF|=(x1+1)(x2+1)=x1x2+x1+x2+1=x1+x2+5
将代入(*)得
| -2(x1+x2)-6 |
| 2(x1+x2)+10 |
| 1 |
| 2 |
这与x1>0且x2>0相矛盾!
经检验,当AB⊥x轴时,θ=2arctan2
| 2 |
| 2 |
| 3 |
综上,θ≠
| 2 |
| 3 |
点评:本题主要考查了直线与抛物线的关系.直线与圆锥曲线的关系是高考的热点问题.试题具有一定的综合性,覆盖面大,不仅考查“三基”掌握的情况,而且重点考查学生的作图、数形结合、等价转化、分类讨论、逻辑推理、合理运算,以及运用数学知识分析问题和解决问题的能力.

练习册系列答案
相关题目