题目内容
两人相约在7:30到8:00之间相遇，早到者应等迟到者10分钟方可离去，如果两人出发是各自独立的，在7:30到8:00之间的任何时刻是等可能的，问两人相遇的可能性有多大 .
解析试题分析：由题意知本题是一个几何概型，试验包含的所有事件是Ω={（x，y）|0＜x＜1 ，0＜y＜1}，做出事件对应的集合表示的面积，写出满足条件的事件是A={（x，y）|0＜x＜1，0＜y＜1，|x-y|＜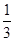
}，算出事件对应的集合表示的面积，根据几何概型概率公式得到结果．解：设两人到达约会地点的时刻分别为x，y，依题意，必须满足|x-y|≤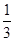才能相遇．我们把他们到达的时刻分别作为横坐标和纵坐标，于是两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内，如图所示，而相遇现象则发生在阴影区域G内，即甲、乙两人的到达时刻（x，y）满足|x-y|≤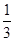，所以两人相遇的概率为区域G与区域Ⅰ的面积之比：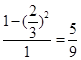
考点：几何概型
点评：本题是一个几何概型，对于这样的问题，一般要通过把试验发生包含的事件同集合结合起来，根据集合对应的图形做出面积，用面积的比值得到结果
练习册系列答案
字词句篇与同步作文达标系列答案
走进文言文系列答案
相关题目
，
，若向区域
上随机投掷一点
，则点
的概率为 ．
{1，2，3，4},若|a
b| 
1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 （分式表示）
服从正态分布
，
，
时，
.
单调递增，则
.
的平均值为
，方差为
，则
的平均值为
，方差为
.
上随机取一个数
，则
的概率为 ．
中，
为
中点，抛物线的一部分在矩形内，点
为抛物线顶点，点
在抛物线上，在矩形内随机地放一点，则此点落在阴影部分的概率为 . 