题目内容
甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为a,再由乙猜甲刚才想的数字,把乙猜的数字记为b,且a,b  {1,2,3,4},若|a
{1,2,3,4},若|a b|
b| 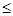 1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 (分式表示)
1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 (分式表示)

解析试题分析:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是两个人分别从4个数字中各选一个数字,共有4×4=16种结果,
满足条件的事件是|a-b|≤1,可以列举出所有的满足条件的事件,
当a=1时,b=1,2,
当a=2时,b=1,2,3
当a=3时,b=2,3,4
当a=4时,b=3,4
总上可知共有2+3+3+2=10种结果,
∴他们“心有灵犀”的概率为 。
。
考点:等可能事件的概率。
点评:简单题,利用分类计数原理计算事件数,关键是注意列举出的事件数做到不重不漏。

练习册系列答案
相关题目
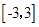 上随机取一个数
上随机取一个数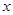 ,使得函数
,使得函数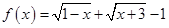 有意义的概率为 .
有意义的概率为 .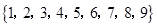 中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 .
中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 . 经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是 ;
经过点B,现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是 ;
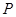 为
为 内一点,且
内一点,且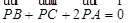 ,现随机将一颗豆子撒在
,现随机将一颗豆子撒在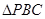 内的概率为 .
内的概率为 .