题目内容
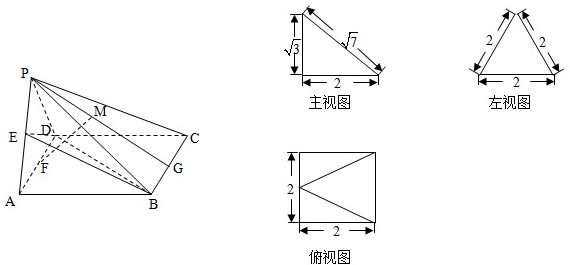
多面体PABCD的直观图及三视图如图所示,E、F、G分别为PA、AD和BC的中点,M为PG上的点,且PM:MG=3;4.
(1)求多面体PABCD的体积;
(2)求证:PC∥平面BDE;
(3)求证:FM⊥平面PBC.
(1)求多面体PABCD的体积;
(2)求证:PC∥平面BDE;
(3)求证:FM⊥平面PBC.

分析:(1)根据几何体的三视图可得四棱锥的高,等边三角形PAD所在平面垂直于边长等于2的正方形ABCD所在平面,再根据棱锥的体积公式求出结果.
(2)设AC和 BD交于点O,则O为正方形ABCD的中心,由OE是三角形PAC的中位线,OE∥AC,利用直线与平面平行的判定定理证得PC∥平面BDE.
(3)连接PF、FG,则BC⊥平面PFG,故BC⊥FM.利用勾股定理证明FM⊥PG,这样,FM垂直于平面PBC 内的两条相交直线PG和BC,由直线与平面垂直的判定定理证得FM⊥平面PBC.
(2)设AC和 BD交于点O,则O为正方形ABCD的中心,由OE是三角形PAC的中位线,OE∥AC,利用直线与平面平行的判定定理证得PC∥平面BDE.
(3)连接PF、FG,则BC⊥平面PFG,故BC⊥FM.利用勾股定理证明FM⊥PG,这样,FM垂直于平面PBC 内的两条相交直线PG和BC,由直线与平面垂直的判定定理证得FM⊥平面PBC.
解答:解:(1)根据几何体的三视图可得多面体PABCD是高为
的四棱锥,
平面PAD垂直于边长等于2的正方形ABCD所在平面,△PAD是等边三角形,
故四棱锥P-ABCD的体积V=
×(2×2)×
=
.
(2)设AC和 BD交于点O,则O为正方形ABCD的中心,又E为PA的中点,
故OE是三角形PAC的中位线,∴OE∥AC.
而OE?平面BDE,AC不在平面BDE内,∴PC∥平面BDE.
(3)连接PF、FG,则BC⊥平面PFG,∴BC⊥FM.△PFG中,PF=
,FG=2,PG=
.
由PM:MG=3:4可得,MG=
,FM=
.∴FM2+MG2=FG2,∴FM⊥PG.
又PG∩BC=G,∴FM⊥平面PBC.
| 3 |
平面PAD垂直于边长等于2的正方形ABCD所在平面,△PAD是等边三角形,
故四棱锥P-ABCD的体积V=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
(2)设AC和 BD交于点O,则O为正方形ABCD的中心,又E为PA的中点,
故OE是三角形PAC的中位线,∴OE∥AC.
而OE?平面BDE,AC不在平面BDE内,∴PC∥平面BDE.
(3)连接PF、FG,则BC⊥平面PFG,∴BC⊥FM.△PFG中,PF=
| 3 |
| 7 |
由PM:MG=3:4可得,MG=
4
| ||
| 7 |
2
| ||
| 7 |
又PG∩BC=G,∴FM⊥平面PBC.
点评:本题主要考查证明线面平行、线面垂直的方法,求棱锥的体积,直线与平面平行的判定以及直线与平面垂直
的判定定理的应用,属于中档题.
的判定定理的应用,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目


 如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),
如图所示,已知多面体PABCD的直观图(图1)和它的三视图(图2),