题目内容
已知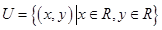 ,
,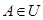 ,
, ,映射
,映射 .对于直线
.对于直线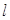 上任意一点
上任意一点 ,
,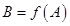 ,若
,若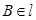 ,我们就称
,我们就称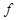 为直线
为直线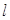 的“相关映射”,
的“相关映射”,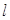 称为映射
称为映射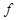 的“相关直线”.又知
的“相关直线”.又知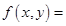
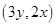 ,则映射
,则映射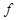 的“相关直线”有多少条( )
的“相关直线”有多少条( )
A.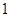 | B.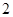 | C. | D.无数 |
B
解析试题分析:当直线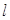 的斜率存在时,不放设直线
的斜率存在时,不放设直线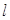 的方程为
的方程为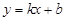 ,
,
设点 的坐标为
的坐标为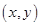 ,且
,且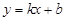 ,则点
,则点 的坐标为
的坐标为 ,
,
由于点 在直线
在直线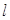 上,则有
上,则有 ,即
,即 ,
,
因此有 ,解得
,解得 ;
;
当直线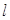 的斜率不存在时,设直线
的斜率不存在时,设直线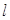 的方程为
的方程为 ,在此直线上任取一点
,在此直线上任取一点 ,则点
,则点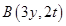 ,
,
由于点 也在直线
也在直线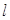 上,因此有
上,因此有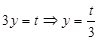 (非定值),此时,直线
(非定值),此时,直线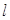 不存在.
不存在.
综上所述,映射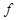 的“相关直线”为
的“相关直线”为 或
或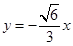 ,有两条,故选B.
,有两条,故选B.
考点:新定义

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案已知 则方程
则方程 所有实根的个数是( )
所有实根的个数是( )
| A.2 | B.3 | C.4 | D.5 |
函数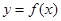 的定义域为
的定义域为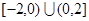 ,其图像上任一点
,其图像上任一点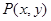 都位于椭圆
都位于椭圆 :
: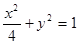 上,下列判断①函数
上,下列判断①函数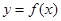 一定是偶函数;②函数
一定是偶函数;②函数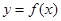 可能既不是偶函数,也不是奇函数;③函数
可能既不是偶函数,也不是奇函数;③函数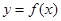 可能是奇函数;④函数
可能是奇函数;④函数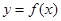 如果是偶函数,则值域是
如果是偶函数,则值域是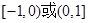 ;⑤函数
;⑤函数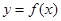 值域是
值域是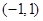 ,则一定是奇函数.其中正确的命题个数有( )个
,则一定是奇函数.其中正确的命题个数有( )个
| A.1 | B.2 | C.3 | D.4 |
下图揭示了一个由区间 到实数集
到实数集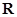 上的对应过程:区间
上的对应过程:区间 内的任意实数
内的任意实数 与数轴上的线段
与数轴上的线段 (不包括端点)上的点
(不包括端点)上的点 一一对应(图一),将线段
一一对应(图一),将线段 围成一个圆,使两端
围成一个圆,使两端 恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 (图三).图三中直线
(图三).图三中直线 与
与 轴交于点
轴交于点 ,由此得到一个函数
,由此得到一个函数 ,则下列命题中正确的序号是 ( )
,则下列命题中正确的序号是 ( ) ;
; 是偶函数;
是偶函数; 在其定义域上是增函数;
在其定义域上是增函数; 的图像关于点
的图像关于点 对称.
对称.
| A.(1)(3)(4) | B.(1)(2)(3) |
| C.(1)(2)(4) | D.(1)(2)(3)(4). |
设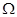 为平面直角坐标系
为平面直角坐标系 中的点集,从
中的点集,从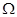 中的任意一点
中的任意一点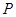 作
作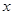 轴、
轴、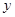 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,
,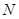 ,记点
,记点 的横坐标的最大值与最小值之差为
的横坐标的最大值与最小值之差为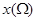 ,点
,点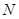 的纵坐标的最大值与最小值之差为
的纵坐标的最大值与最小值之差为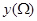 .如果
.如果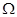 是边长为1的正方形,那么
是边长为1的正方形,那么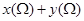 的取值范围是( )
的取值范围是( )
A.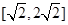 | B.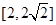 | C.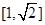 | D.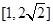 |
已知函数y=f(x)是定义在R上的增函数,函数y=f(x-1)的图象关于点(1,0)对称.若对任意的x,y∈R,不等式f(x2-6x+21)+f(y2-8y)<0恒成立,则当x>3时,x2+y2的取值范围是 ( ).
| A.(3,7) | B.(9,25) | C.(13,49) | D.(9, 49) |
方程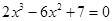 在
在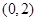 内根的个数有( )
内根的个数有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
(2014·长沙模拟)某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
| A.45.606万元 | B.45.6万元 |
| C.45.56万元 | D.45.51万元 |
下列函数中,既是偶函数又在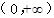 单调递增的函数是
单调递增的函数是
A.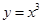 | B.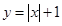 | C.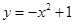 | D.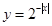 |