题目内容
设{x}表示离x最近的整数,即若m-| 1 |
| 2 |
| 1 |
| 2 |
下面是关于函数f(x)=|x-{x}|的四个命题:①函数y=f(x)的定义域是R,值域是[0,
| 1 |
| 2 |
| k |
| 2 |
分析:①定义域、值域可由题意直接得到.
②通过验证f(
+x)=f(
-x)可知正确.
③由f(x+1)=|x+1-{x+1}|=|x-{x}}=f(x)可直接验证.
②通过验证f(
| k |
| 2 |
| k |
| 2 |
③由f(x+1)=|x+1-{x+1}|=|x-{x}}=f(x)可直接验证.
解答:解:①根据题意可直接得到定义域为R,值域为[0,
]
②验证f(
+x)=f(
-x)正确性即可
当k为偶数时,
为整数,∵f(
+x)=|
+x-{
+x}|=|x-{x}|
f(
-x)=|
-x-{
-x}|=|-x+{x}|=|x-{x}|=f(
+x)
当k为奇数时,
为整数
∵f(
+x)=|
+
+x-{
+
+x}|=|
+x-{
+x}|=|x-{x}|
f(
-x)=|
+
-x-{
+
-x}|=|
-x-{
-x}|=|x-{x}|=f(
+x)
y=f(x)的图象关于直线x=
对称.
③∵f(x+1)=|x+1-{x+1}|=|x-{x}}=f(x)
∴f(x)是周期函数且最小正周期是1
故答案为:①②③
| 1 |
| 2 |
②验证f(
| k |
| 2 |
| k |
| 2 |
当k为偶数时,
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
f(
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
| k |
| 2 |
当k为奇数时,
| k-1 |
| 2 |
∵f(
| k |
| 2 |
| k-1 |
| 2 |
| 1 |
| 2 |
| k-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
f(
| k |
| 2 |
| k-1 |
| 2 |
| 1 |
| 2 |
| k-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
y=f(x)的图象关于直线x=
| k |
| 2 |
③∵f(x+1)=|x+1-{x+1}|=|x-{x}}=f(x)
∴f(x)是周期函数且最小正周期是1
故答案为:①②③
点评:本题主要考查函数的基本性质--定义域、值域、对称性、周期性.另外,函数的奇偶性、单调性也是经常被考到的对象,要引起重视.

练习册系列答案
相关题目
 ,则{x}=m.
,则{x}=m. ;②函数y=f(x)的图象关于直线
;②函数y=f(x)的图象关于直线 对称;③函数y=f(x)是周期函数,最小正周期是1;其中正确的命题序号是 .
对称;③函数y=f(x)是周期函数,最小正周期是1;其中正确的命题序号是 . ,则{x}=m.
,则{x}=m.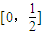 ;②函数y=f(x)的图象关于直线
;②函数y=f(x)的图象关于直线 对称;③函数y=f(x)是周期函数,最小正周期是1;其中正确的命题序号是 .
对称;③函数y=f(x)是周期函数,最小正周期是1;其中正确的命题序号是 .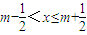 ,则{x}=m.
,则{x}=m. ;②函数y=f(x)的图象关于直线
;②函数y=f(x)的图象关于直线 对称;③函数y=f(x)是周期函数,最小正周期是1;其中正确的命题序号是 .
对称;③函数y=f(x)是周期函数,最小正周期是1;其中正确的命题序号是 .