题目内容
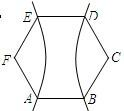
如图,ABCDEF为正六边形,则以F、C为焦点,且经过A、E、D、B四点的双曲线的离心率为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
分析:设正六边形ABCDEF的边长是2,以FC为x礼貌,FC的垂直平分线为y轴,建立平面直角坐标系,求出D,F,C的坐标后,a=
×(|DF|-|DC|),从而求出双曲线的离心率.
| 1 |
| 2 |
解答:解:设正六边形ABCDEF的边长是2,
以FC为x轴,FC的垂直平分线为y轴,建立平面直角坐标系,
则D(1,
),F(-2,0),C(2,0),
∴|DF|= 2
, |DC|=2,
∴a=
-1,c=2,
∴e=
=
+1.
故选D.
以FC为x轴,FC的垂直平分线为y轴,建立平面直角坐标系,
则D(1,
| 3 |
∴|DF|= 2
| 3 |
∴a=
| 3 |
∴e=
| 2 | ||
|
| 3 |
故选D.
点评:恰当建立空间直角坐标系是准确题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目



















