题目内容
已知平面 平面
平面 ,
, ,线段
,线段 与线段
与线段 交于点
交于点 ,若
,若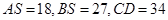 ,则
,则 = ( )
= ( )
A. | B. | C. | D. |
B
解析试题分析::①若S点位于平面α与平面β之间,根据平面平行的性质定理,得,AC∥BD,∴ ,即
,即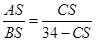 ,∴CS=
,∴CS= .
.
②若S点位于平面α与平面β外,根据平面平行的性质,得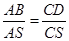
,∴CS=68故答案为 或68.选B.
或68.选B.
考点:本题主要是考查平面平行的性质定理,做题时容易丢情况,需谨慎.
点评:解决该试题的关键是因为平面α∥平面β,利用平面平行的性质定理,可得,AC∥BD,再根据S点的位置,利用成比例线段,就可求出CS的值

练习册系列答案
相关题目
如果对于空间任意n(n≥2)条直线总存在一个平面α,使得这n条直线与平面α所成的角均相等,那么这样的n( )
| A.最大值为3 | B.最大值为4 | C.最大值为5 | D.不存在最大值 |
二面角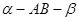 的平面角是锐角,点C
的平面角是锐角,点C 且点C不在棱AB上,D是C在平面
且点C不在棱AB上,D是C在平面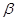 上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
上的射影,E是棱AB上满足∠CEB为锐角的任意一点,则( )
| A.∠CEB>∠DEB | B.∠CEB=∠DEB |
| C.∠CEB<∠DEB | D.∠CEB与∠DEB的大小关系不能确定 |
有两条不同的直线m,n与两个不同的平面α,β,下列命题正确的是( ).
| A.m∥α,n∥β,且α∥β,则m∥n |
| B.m⊥α,n⊥β,且α⊥β,则m∥n |
| C.m∥α,n⊥β,且α⊥β,则m∥n |
| D.m⊥α,n∥β,且α∥β,则m⊥n |
已知空间三条直线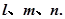 若
若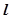 与
与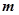 异面,且
异面,且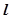 与
与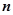 异面,则( )
异面,则( )
A.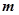 与 与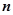 异面. 异面. | B.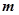 与 与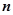 相交. 相交. |
C.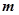 与 与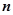 平行. 平行. | D.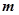 与 与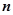 异面、相交、平行均有可能. 异面、相交、平行均有可能. |
不同的直线a, b, c及不同的平面α,β,γ,下列命题正确的是( )
A.若a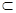 α,b α,b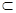 α,c⊥a, c⊥b 则c⊥α α,c⊥a, c⊥b 则c⊥α |
B.若b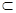 α, a//b则 a//α α, a//b则 a//α |
| C.若a⊥α, b⊥α 则a//b |
| D.若a//α,α∩β=b则a//b |
 侧棱长为
侧棱长为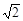 ,底面边长为
,底面边长为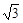 ,
, 是
是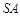 的中点,则异面直线
的中点,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )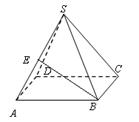


 中,下列几种说法正确的是 ( )
中,下列几种说法正确的是 ( )

 与
与 成
成 角
角 与
与 成
成 角
角
 的正方形
的正方形 沿对角线
沿对角线 成直二面角(平面
成直二面角(平面 平面
平面 ),则
),则 的度数是( )
的度数是( ) B.
B.  C.
C.  D
D 