题目内容
对定义在实数集R上的函数f1(x),f2(x),令F(x)=f1(x)+f2(x),已知对任意不同的实数x1,x2,|f1(x1)-f1(x2)|>|f2(x1)-f2(x2)|.
(1)若y=f1(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(2)若y=f2(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(3)求函数f(x)=x2+
(x>0)的单调区间.
(1)若y=f1(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(2)若y=f2(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(3)求函数f(x)=x2+
| 1 |
| 4x |
(1)设x1<x2由y=f1(x)是区间D上的增函数可得f1(x1)<f1(x2)
①若f2(x)为单调递增或常函数,则y=F(x)是区间D上的增函数
②若函数f2(x1)>f2(x2),则由|f1(x1)-f1(x2)|>|f2(x1)-f2(x2)|可得,-f1(x1)+f1(x2)|>f2(x1)-f2(x2)
∴f1(x1)+f2(x1)<f1(x2)+f2(x2)即F(x1)<F(x2)
综上可得函数F(X)为单调递增的函数
(2)例如函数f1(x)=-3x,f2(x)=2x,则F(x)=2x-3x不是单调递增函数
(3)f′(x)=2x-
=
∵x>0由f′(x)≥0可得x≥
,f′(x)<0可得0<x<
函数f(x)的单调增区间是[
,+∞),单调减区间是(0,
)
①若f2(x)为单调递增或常函数,则y=F(x)是区间D上的增函数
②若函数f2(x1)>f2(x2),则由|f1(x1)-f1(x2)|>|f2(x1)-f2(x2)|可得,-f1(x1)+f1(x2)|>f2(x1)-f2(x2)
∴f1(x1)+f2(x1)<f1(x2)+f2(x2)即F(x1)<F(x2)
综上可得函数F(X)为单调递增的函数
(2)例如函数f1(x)=-3x,f2(x)=2x,则F(x)=2x-3x不是单调递增函数
(3)f′(x)=2x-
| 1 |
| 4x2 |
| 8x3-1 |
| 4x2 |
∵x>0由f′(x)≥0可得x≥
| 1 |
| 2 |
| 1 |
| 2 |
函数f(x)的单调增区间是[
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
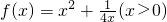 的单调区间.
的单调区间.